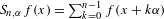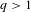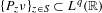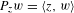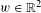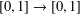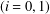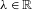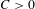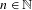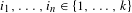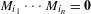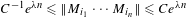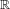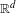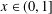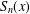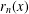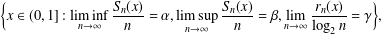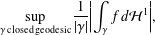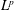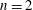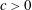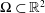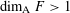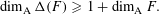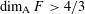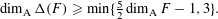Refine listing
Actions for selected content:
352 results in 28Axx
Fast and slow points of Birkhoff sums
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3236-3256
- Print publication:
- December 2020
-
- Article
- Export citation
On self-similar measures with absolutely continuous projections and dimension conservation in each direction
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 26 June 2019, pp. 3438-3456
- Print publication:
- December 2020
-
- Article
- Export citation
PACKING SUBORDINACY WITH APPLICATION TO SPECTRAL CONTINUITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 13 June 2019, pp. 226-244
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Topological Properties of a Class of Higher-dimensional Self-affine Tiles
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 727-740
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
On the existence of cocycle-invariant Borel probability measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 12 April 2019, pp. 3150-3168
- Print publication:
- November 2020
-
- Article
- Export citation
SYMMETRIC ITINERARY SETS: ALGORITHMS AND NONLINEAR EXAMPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 109-118
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
SYMMETRIC ITINERARY SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 06 March 2019, pp. 97-108
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Uniformity of Lyapunov exponents for non-invertible matrices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 2399-2433
- Print publication:
- September 2020
-
- Article
- Export citation
A NOTE ON THE INTERSECTIONS OF THE BESICOVITCH SETS AND ERDŐS–RÉNYI SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 33-45
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
A COMPACTNESS PRINCIPLE FOR MAXIMISING SMOOTH FUNCTIONS OVER TOROIDAL GEODESICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 148-154
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Explicit Salem sets, Fourier restriction, and metric Diophantine approximation in the p-adic numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1265-1288
- Print publication:
- June 2020
-
- Article
- Export citation
The quasi-Assouad dimension of stochastically self-similar sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 261-275
- Print publication:
- February 2020
-
- Article
- Export citation
An Endpoint Alexandrov Bakelman Pucci Estimate in the Plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 643-651
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Digit frequencies and self-affine sets with non-empty interior
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1755-1787
- Print publication:
- July 2020
-
- Article
- Export citation
DIMENSIONS OF TRIANGLE SETS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 18 December 2018, pp. 311-332
- Print publication:
- 2019
-
- Article
- Export citation
A new class of costs for optimal transport planning
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1229-1263
-
- Article
-
- You have access
- Export citation
Dilation volumes of sets of finite perimeter
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1095-1118
- Print publication:
- December 2018
-
- Article
- Export citation
Renewal theorems for processes with dependent interarrival times
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1193-1216
- Print publication:
- December 2018
-
- Article
- Export citation
Metrical Results on the Distribution of Fractional Parts of Powers of Real Numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 505-521
-
- Article
- Export citation
Assouad Dimension of Random Processes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 281-290
-
- Article
- Export citation