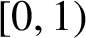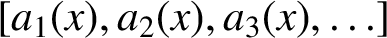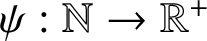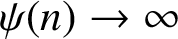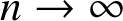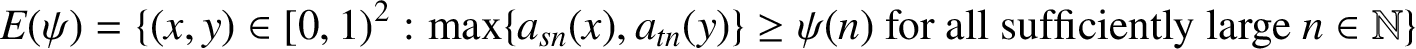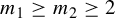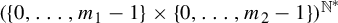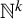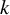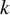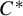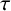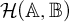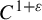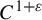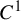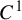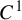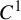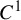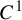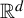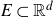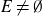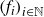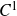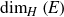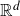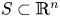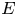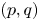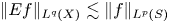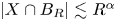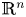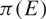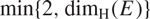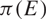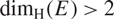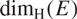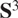Refine listing
Actions for selected content:
354 results in 28Axx
ON THE INCREASING PARTIAL QUOTIENTS OF CONTINUED FRACTIONS OF POINTS IN THE PLANE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 404-411
- Print publication:
- June 2022
-
- Article
- Export citation
Dimensions of ‘self-affine sponges’ invariant under the action of multiplicative integers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 14 December 2021, pp. 417-459
- Print publication:
- February 2023
-
- Article
- Export citation
DENSITY-LIKE AND GENERALIZED DENSITY IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 November 2021, pp. 228-251
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable intersections of conformal Cantor sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 25 October 2021, pp. 1-49
- Print publication:
- January 2023
-
- Article
- Export citation
Cocycles on groupoids arising from
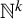 $\mathbb {N}^k$-actions
$\mathbb {N}^k$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3325-3356
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A DIMENSIONAL RESULT ON THE PRODUCT OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 357-385
- Print publication:
- December 2022
-
- Article
- Export citation
ON SEQUENCES OF HOMOMORPHISMS INTO MEASURE ALGEBRAS AND THE EFIMOV PROBLEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 September 2021, pp. 191-218
- Print publication:
- March 2023
-
- Article
- Export citation
Hausdorff and packing dimensions and measures for nonlinear transversally non-conformal thin solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3458-3489
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dimension estimates for
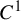 $C^1$ iterated function systems and repellers. Part II
$C^1$ iterated function systems and repellers. Part II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3357-3392
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lorentz and Gale–Ryser theorems on general measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 August 2021, pp. 857-878
- Print publication:
- August 2022
-
- Article
- Export citation
The scenery flow of self-similar measures with weak separation condition
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 3167-3190
- Print publication:
- October 2022
-
- Article
- Export citation
Random fractals and their intersection with winning sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 07 July 2021, pp. 655-684
- Print publication:
- May 2022
-
- Article
- Export citation
Optimal transportation and stationary measures for iterated function systems
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 28 June 2021, pp. 163-187
- Print publication:
- July 2022
-
- Article
- Export citation
A new proof of the dimension gap for the Gauss map
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 43-71
- Print publication:
- January 2022
-
- Article
- Export citation
Density theorems for anisotropic point configurations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 1244-1276
- Print publication:
- October 2022
-
- Article
- Export citation
Fourier restriction in low fractal dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 373-407
-
- Article
- Export citation
Continuity of Hausdorff dimension across generic dynamical Lagrange and Markov spectra II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 1898-1907
- Print publication:
- June 2022
-
- Article
- Export citation
Porosity in Conformal Dynamical Systems
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 14 April 2021, pp. 303-371
- Print publication:
- March 2022
-
- Article
- Export citation
On the dimension of points which escape to infinity at given rate under exponential iteration
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 29 March 2021, pp. 1591-1623
- Print publication:
- May 2022
-
- Article
- Export citation
Projections of Poisson cut-outs in the Heisenberg group and the visual 3-sphere
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
- Export citation