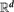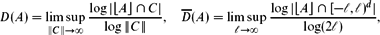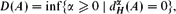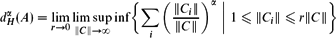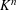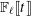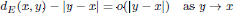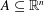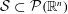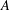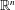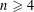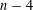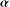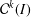Refine listing
Actions for selected content:
352 results in 28Axx
A Fractal Operator on Some Standard Spaces of Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 771-786
-
- Article
- Export citation
BOUNDARY PARAMETRIZATION AND THE TOPOLOGY OF TILES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 127-164
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
ON POINTS WITH POSITIVE DENSITY OF THE DIGIT SEQUENCE IN INFINITE ITERATED FUNCTION SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 435-443
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
CONTINUITY OF THE HAUSDORFF DIMENSION FOR GRAPH-DIRECTED SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 471-478
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Influence in product spaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 145-152
- Print publication:
- July 2016
-
- Article
- Export citation
A NEW EXAMPLE OF A DETERMINISTIC CHAOS GAME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 02 June 2016, pp. 464-470
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Mappings of Lp-integrable distortion: regularity of the inverse
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 647-663
- Print publication:
- June 2016
-
- Article
- Export citation
Multiple Spectra of Bernoulli Convolutions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 187-202
-
- Article
- Export citation
EXPECTATIONS OVER DETERMINISTIC FRACTAL SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 25 April 2016, pp. 171-172
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Compact embedding results of Sobolev spaces and positive solutions to an elliptic equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 11 April 2016, pp. 693-721
- Print publication:
- August 2016
-
- Article
- Export citation
Marstrand-type Theorems for the Counting and Mass Dimensions in ℤ
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 700-743
-
- Article
- Export citation
A general formula for the anisotropic outer Minkowski content of a set
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 393-413
- Print publication:
- April 2016
-
- Article
- Export citation
RESOLVABILITY OF MEASURABLE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 70-79
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
KAKEYA-TYPE SETS IN LOCAL FIELDS WITH FINITE RESIDUE FIELD
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 614-629
- Print publication:
- 2016
-
- Article
- Export citation
Some new results about the geometry of sets of finite perimeter
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 23 December 2015, pp. 79-105
- Print publication:
- February 2016
-
- Article
- Export citation
On the singular components of a copula
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1175-1182
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
LOCAL SET APPROXIMATION: MATTILA–VUORINEN TYPE SETS, REIFENBERG TYPE SETS, AND TANGENT SETS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 30 October 2015, e24
-
- Article
-
- You have access
- Open access
- Export citation
RESOLVABILITY PROPERTIES OF SIMILAR TOPOLOGIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 September 2015, pp. 470-477
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
FRACTAL BASES FOR BANACH SPACES OF SMOOTH FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 405-419
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A NOTE ON SOME TOPOLOGICAL PROPERTIES OF SETS WITH FINITE PERIMETER
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 23 July 2015, pp. 637-647
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
 , the space of all real-valued continuous functions defined on a compact interval
, the space of all real-valued continuous functions defined on a compact interval 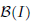 of all bounded functions and the Lebesgue space
of all bounded functions and the Lebesgue space 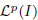 , and in some standard spaces of smooth functions such as the space
, and in some standard spaces of smooth functions such as the space 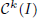 of
of 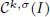 and Sobolev spaces
and Sobolev spaces 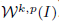 . Using properties of the
. Using properties of the 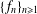
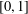
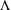
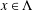
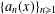

 be an open set in ℝ
be an open set in ℝ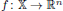 is a Sobolev homeomorphism. We study the regularity of
is a Sobolev homeomorphism. We study the regularity of 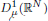 of the commonly used Sobolev space
of the commonly used Sobolev space 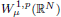 to
to