Refine listing
Actions for selected content:
352 results in 28Axx
Families of surfaces lying in a null set
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-162
- Print publication:
- December 2004
-
- Article
- Export citation
Multiplicities of Higher Lie Characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-21
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Engel Series Expansions of Laurent Series and Hausdorff Dimensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-7
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Joint continuity of injective tensor products of vector measures in Banach lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-200
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Thick and thin points for random recursive fractals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 251-277
- Print publication:
- March 2003
-
- Article
- Export citation
Sums of Cantor sets yielding an interval
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-418
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Average co-ordinate entropy
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-186
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
Generalized vector multiplicative cascades
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 874-895
- Print publication:
- December 2001
-
- Article
- Export citation
Random fractals and probability metrics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 925-947
- Print publication:
- December 2000
-
- Article
- Export citation
N-fold sums of Cantor sets
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 243-250
- Print publication:
- December 2000
-
- Article
- Export citation
Density and covering properties of intervals of ℝn
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-242
- Print publication:
- December 2000
-
- Article
- Export citation
Fubini-type theorems for general measure constructions
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-265
- Print publication:
- December 2000
-
- Article
- Export citation
A central limit theorem for iterated random functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 748-755
- Print publication:
- September 2000
-
- Article
- Export citation
Compact measure spaces
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 331-336
- Print publication:
- December 1999
-
- Article
- Export citation
On the convergence of Σ∞n = 1f(nx) for measurable functions
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 337-341
- Print publication:
- December 1999
-
- Article
- Export citation
Fractal n-hedral tilings of ℝd
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-417
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
The convex hull of samples from self-similar distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 34-47
- Print publication:
- March 1999
-
- Article
- Export citation
Hausdorff and packing dimensions and sections of measures
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-77
- Print publication:
- June 1998
-
- Article
- Export citation
No b-concentrated measures whenever 1<b≤2
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-41
- Print publication:
- June 1998
-
- Article
- Export citation
A relationship between packing and topological dimensions
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-53
- Print publication:
- June 1998
-
- Article
- Export citation
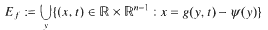
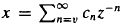 in an inderminate
in an inderminate 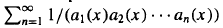 be the Engel expansin of Laurent series of
be the Engel expansin of Laurent series of 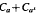 is an interval if and only if a /(1−2
is an interval if and only if a /(1−2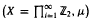 is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and
is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and 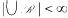 , then there is a finite sequence
, then there is a finite sequence 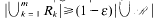 and
and 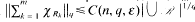 .
.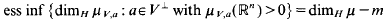
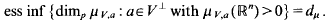
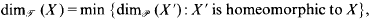
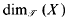 and
and 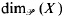 denote the topological and packing dimensions of
denote the topological and packing dimensions of 