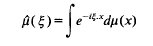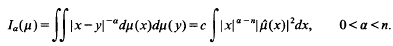Refine listing
Actions for selected content:
352 results in 28Axx
Average densities and linear rectifiability of measures
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 313-324
- Print publication:
- December 1997
-
- Article
- Export citation
On some regularity conditions of Borel measures on R
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 218-224
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
All-sum sets in (0,1]—Category and measure
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 61-87
- Print publication:
- June 1997
-
- Article
- Export citation
Measurable Hilbert sheaves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-215
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
On products of almost strong liftings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 311-333
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
Order-two density and the strong law of large numbers
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-22
- Print publication:
- June 1996
-
- Article
- Export citation
The Gaussian distribution revisited
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 500-524
- Print publication:
- June 1996
-
- Article
- Export citation
Epsilon entropy and the packing of balls in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 23-31
- Print publication:
- June 1996
-
- Article
- Export citation
On improvements of the order of approximation in the Poisson limit theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 146-155
- Print publication:
- March 1996
-
- Article
- Export citation
Solving the inverse problem for measures using iterated function systems: a new approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 800-820
- Print publication:
- September 1995
-
- Article
- Export citation
On the existence of subsets of finite positive packing measure
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-24
- Print publication:
- June 1995
-
- Article
- Export citation
Order-two density of sets and measures with non-integral dimension
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-14
- Print publication:
- June 1995
-
- Article
- Export citation
Unions of products of independent sets
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-29
- Print publication:
- June 1995
-
- Article
- Export citation
Complex extreme measurable selections
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 222-231
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
Insertion of a measurable function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-304
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Dimension prints of fractal sets
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-94
- Print publication:
- June 1994
-
- Article
- Export citation
Sur une procédure de branchement déterministe et ses dérivées aléatoires
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 333-347
- Print publication:
- June 1994
-
- Article
- Export citation
On lattice-perfect measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-182
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Estimates of spherial averages of Fourier transforms and dimensions of sets
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 322-330
- Print publication:
- December 1993
-
- Article
- Export citation
Paradoxical decompositions using Lipschitz functions
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-222
- Print publication:
- December 1992
-
- Article
- Export citation
 and its resulting all-sums set
and its resulting all-sums set  We show further that structured all-sums sets with positive measure are not partition regular even if one allows shifted all-sums sets. That is, we produce a two cell measurable partition of (0, 1 ] such that neither set contains a translate of any structured all-sums set with positive measure.
We show further that structured all-sums sets with positive measure are not partition regular even if one allows shifted all-sums sets. That is, we produce a two cell measurable partition of (0, 1 ] such that neither set contains a translate of any structured all-sums set with positive measure.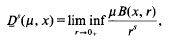
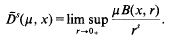
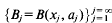 be a sequence of mutually disjoint open balls, with centres
be a sequence of mutually disjoint open balls, with centres 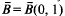 in
in 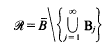
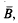 the balls {
the balls {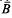 provided that λ(ℛ)=0, where λ denotes the
provided that λ(ℛ)=0, where λ denotes the 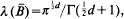 henceforth denoted by
henceforth denoted by 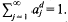 Larman [11] has noted that, under these circumstances, one also has
Larman [11] has noted that, under these circumstances, one also has 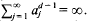 .
.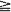 1, with invariant measures for iterated function systems by matching its moments. There are two novel features in our treatment. 1. An infinite set of fixed affine contraction maps on
1, with invariant measures for iterated function systems by matching its moments. There are two novel features in our treatment. 1. An infinite set of fixed affine contraction maps on 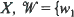 ,
, 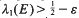 and
and 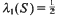 and
and 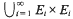 where the sets
where the sets 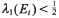 . The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.
. The results of this paper answer questions of M. Laczkovich and are related to a paper of D. H. Fremlin.