Refine listing
Actions for selected content:
59 results in 11Hxx
A sieve algorithm based on overlattices
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 49-70
-
- Article
-
- You have access
- Export citation
CONVEX CURVES AND A POISSON IMITATION OF LATTICES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 139-152
- Print publication:
- January 2014
-
- Article
- Export citation
SLIDE REDUCTION, SUCCESSIVE MINIMA AND SEVERAL APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 30 April 2013, pp. 390-406
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
On a lattice point problem arising in the spectral analysis of periodic operators
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-98
- Print publication:
- December 2003
-
- Article
- Export citation
Non-linear boundary value problems on the semi-infinite interval: an upper and lower solution approach
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-140
- Print publication:
- June 2002
-
- Article
- Export citation
Small positive values of indefinite ternary forms
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-196
- Print publication:
- June 2002
-
- Article
- Export citation
Quick asymptotic upper bounds for lattice kissing numbers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-57
- Print publication:
- June 2002
-
- Article
- Export citation
Double circulant constructions of the Leech lattice
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-297
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
Lattice packing of spheres and the Wulff-Shape
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-236
- Print publication:
- December 1996
-
- Article
- Export citation
Bounds on the covering radius of a lattice
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-164
- Print publication:
- June 1996
-
- Article
- Export citation
Low dimensional lattices have a strict Voronoï basis
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-238
- Print publication:
- December 1995
-
- Article
- Export citation
A lattice without a basis of minimal vectors
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 175-177
- Print publication:
- June 1995
-
- Article
- Export citation
On Mahler's compound bodies
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-215
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
A bound, and a conjecture, on the maximum lattice-packing density of a superball
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-143
- Print publication:
- June 1993
-
- Article
- Export citation
Uniform distribution and lattice point counting
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-50
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
Constructive packings of cross polytopes
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 376-380
- Print publication:
- December 1991
-
- Article
- Export citation
The dual lattice of an extreme six-dimensional lattice
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 373-383
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
A note on lattices of rational functions
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-13
- Print publication:
- June 1991
-
- Article
- Export citation
The Coset lattices of E. S. Barnes and G. E. Wall
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 418-433
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation

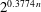
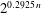
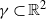
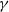


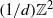
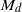
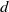
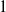
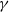
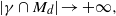
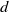
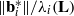
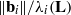
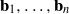
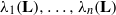
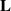
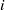
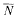 (ρ) the number
(ρ) the number 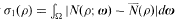 for dimensions
for dimensions 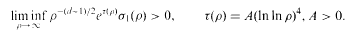
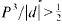 .
.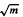 in the Leech lattice. We give such a construction by means of double circulant codes whenever
in the Leech lattice. We give such a construction by means of double circulant codes whenever 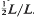 . The convex hull of all minimal vectors of a class
. The convex hull of all minimal vectors of a class 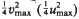 be a maximal squared radius of
be a maximal squared radius of 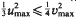 , then
, then 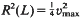 . This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise,
. This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise, 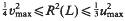 . This is a refinement of a result of Norton ([3], Ch. 22).
. This is a refinement of a result of Norton ([3], Ch. 22).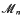 . This is then used to prove that a Minkowski reduced basis of a lattice of dimension
. This is then used to prove that a Minkowski reduced basis of a lattice of dimension 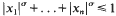 is 2
is 2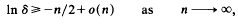
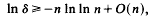
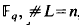 ,
, 