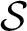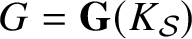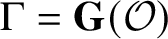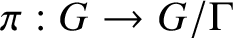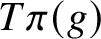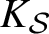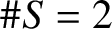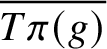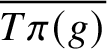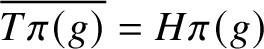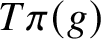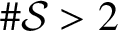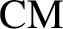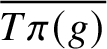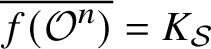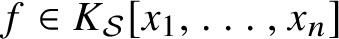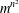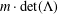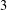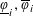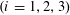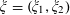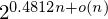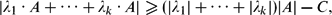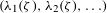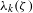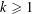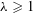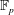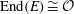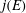Refine listing
Actions for selected content:
59 results in 11Hxx
Closures of locally divergent orbits of maximal tori and values of homogeneous forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3142-3177
- Print publication:
- October 2021
-
- Article
- Export citation
Number-theoretic positive entropy shifts with small centralizer and large normalizer
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2020, pp. 3201-3226
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
CLASSIFICATION OF THE SUBLATTICES OF A LATTICE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 50-61
- Print publication:
- February 2021
-
- Article
- Export citation
On intrinsic and extrinsic rational approximation to Cantor sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 10 February 2020, pp. 1560-1589
- Print publication:
- May 2021
-
- Article
- Export citation
Primitive Points in Rational Polygons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 850-870
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Higher-rank Bohr sets and multiplicative diophantine approximation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 24 September 2019, pp. 2214-2233
- Print publication:
- November 2019
-
- Article
- Export citation
Primes Dividing Invariants of CM Picard Curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 480-504
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Eigenvalue Optimisation on Flat Tori and Lattice Points in Anisotropically Expanding Domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 967-987
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
CENTRAL LIMIT THEOREM FOR PLANCK-SCALE MASS DISTRIBUTION OF TORAL LAPLACE EIGENFUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 643-676
- Print publication:
- 2019
-
- Article
- Export citation
TRIANGLES CAPTURING MANY LATTICE POINTS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 551-582
- Print publication:
- 2018
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
PARAMETRIC GEOMETRY OF NUMBERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1114-1135
- Print publication:
- 2017
-
- Article
- Export citation
SIMULTANEOUS APPROXIMATION TO TWO REALS: BOUNDS FOR THE SECOND SUCCESSIVE MINIMUM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1136-1151
- Print publication:
- 2017
-
- Article
- Export citation
Tuple lattice sieving
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 146-162
-
- Article
-
- You have access
- Export citation
A GENERALIZATION OF THE DISCRETE VERSION OF MINKOWSKI’S FUNDAMENTAL THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 29 February 2016, pp. 637-652
- Print publication:
- 2016
-
- Article
- Export citation
Sum of Many Dilates
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 08 September 2015, pp. 460-469
-
- Article
- Export citation
ON THE SPECTRUM OF DIOPHANTINE APPROXIMATION CONSTANTS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 June 2015, pp. 79-100
- Print publication:
- 2016
-
- Article
- Export citation
Effective limit distribution of the Frobenius numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 898-916
- Print publication:
- May 2015
-
- Article
- Export citation
Constructing supersingular elliptic curves with a given endomorphism ring
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 71-91
-
- Article
-
- You have access
- Export citation
Approximating the densest sublattice from Rankin’s inequality
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 92-111
-
- Article
-
- You have access
- Export citation