Refine listing
Actions for selected content:
556 results in 90Bxx
Buffer content of a leaky-bucket system with long-range dependent input traffic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 581-601
- Print publication:
- September 2003
-
- Article
- Export citation
An inspection–repair–replacement model for a deteriorating system with unobservable state
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1031-1042
- Print publication:
- September 2003
-
- Article
- Export citation
On the collapsibility of lifetime regression models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 755-772
- Print publication:
- September 2003
-
- Article
- Export citation
Generalized processor sharing queues with heterogeneous traffic classes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 806-845
- Print publication:
- September 2003
-
- Article
- Export citation
A reduced-peak equivalence for queues with a mixture of light-tailed and heavy-tailed input flows
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 793-805
- Print publication:
- September 2003
-
- Article
- Export citation
Stationary iterated tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 337-353
- Print publication:
- June 2003
-
- Article
- Export citation
On stability of queueing networks with job deadlines
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 293-304
- Print publication:
- June 2003
-
- Article
- Export citation
Polling systems with periodic server routeing in heavy traffic: distribution of the delay
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 305-326
- Print publication:
- June 2003
-
- Article
- Export citation
Average cost under the P M λ, τ policy in a finite dam with compound Poisson inputs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 519-526
- Print publication:
- June 2003
-
- Article
- Export citation
Characterizations of classes of lifetime distributions generalizing the NBUE class
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 20-32
- Print publication:
- March 2003
-
- Article
- Export citation
Characterizing losses during busy periods in finite buffer systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 242-249
- Print publication:
- March 2003
-
- Article
- Export citation
Some memoryless bandit policies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 250-256
- Print publication:
- March 2003
-
- Article
- Export citation
Recursive filters for a partially observable system subject to random failure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 207-227
- Print publication:
- March 2003
-
- Article
- Export citation
Asymptotic failure rate of a Markov deteriorating system with preventive maintenance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-19
- Print publication:
- March 2003
-
- Article
- Export citation
Asymptotic independence and a network traffic model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 671-699
- Print publication:
- December 2002
-
- Article
- Export citation
Availability of periodically inspected systems subject to Markovian degradation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 700-711
- Print publication:
- December 2002
-
- Article
- Export citation
Index policies for a class of discounted restless bandits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 754-774
- Print publication:
- December 2002
-
- Article
- Export citation
On bounds for some optimal policies in reliability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 491-502
- Print publication:
- September 2002
-
- Article
- Export citation
On a tandem G-network with blocking
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 626-661
- Print publication:
- September 2002
-
- Article
- Export citation
Poisson traffic flow in a general feedback queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 3 / September 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 630-636
- Print publication:
- September 2002
-
- Article
- Export citation
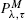 policy in a finite dam in which the input of water is formed by a compound Poisson process and the rate of water release is changed instantaneously from
policy in a finite dam in which the input of water is formed by a compound Poisson process and the rate of water release is changed instantaneously from 