Refine listing
Actions for selected content:
556 results in 90Bxx
Explicit criteria for several types of ergodicity of the embedded M/G/1 and GI/M/n queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 778-790
- Print publication:
- September 2004
-
- Article
- Export citation
A second-order Markov-modulated fluid queue with linear service rate
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 758-777
- Print publication:
- September 2004
-
- Article
- Export citation
Network decomposition in the many-sources regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 893-918
- Print publication:
- September 2004
-
- Article
- Export citation
Adaptive simulation using perfect control variates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 859-876
- Print publication:
- September 2004
-
- Article
- Export citation
Cyclic queueing networks with subexponential service times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 791-801
- Print publication:
- September 2004
-
- Article
- Export citation
Decomposition property in a discrete-time queue with multiple input streams and service interruptions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 524-534
- Print publication:
- June 2004
-
- Article
- Export citation
Technology diffusion by learning from neighbours
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 355-376
- Print publication:
- June 2004
-
- Article
- Export citation
Poisson approximation for some point processes in reliability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 455-470
- Print publication:
- June 2004
-
- Article
- Export citation
Tail asymptotics for processor-sharing queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 525-543
- Print publication:
- June 2004
-
- Article
- Export citation
Characterization and sufficient conditions for normed ergodicity of Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 227-242
- Print publication:
- March 2004
-
- Article
- Export citation
On the optimal allocation of service to impatient tasks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 51-72
- Print publication:
- March 2004
-
- Article
- Export citation
Optimal control of a flexible server
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 139-170
- Print publication:
- March 2004
-
- Article
- Export citation
A note on the waiting time in M[X]/G/1 queueing systems with a removable server
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 287-291
- Print publication:
- March 2004
-
- Article
- Export citation
Estimating tail decay for stationary sequences via extreme values
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 198-226
- Print publication:
- March 2004
-
- Article
- Export citation
On-line parameter estimation for a failure-prone system subject to condition monitoring
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 211-220
- Print publication:
- March 2004
-
- Article
- Export citation
Analysis of R-out-of-N repairable systems: the case of phase-type distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 116-138
- Print publication:
- March 2004
-
- Article
- Export citation
Minimal repair in heterogeneous populations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 281-286
- Print publication:
- March 2004
-
- Article
- Export citation
Between the expert and majority rules
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 4 / December 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 941-960
- Print publication:
- December 2003
-
- Article
- Export citation
Algorithmic analysis of the BMAP/D/k system in discrete time
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 4 / December 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1131-1152
- Print publication:
- December 2003
-
- Article
- Export citation
Carousel system performance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 602-612
- Print publication:
- September 2003
-
- Article
- Export citation
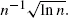 A similar estimator converges at rate
A similar estimator converges at rate 