Refine listing
Actions for selected content:
556 results in 90Bxx
Dynamic Distributed Scheduling in Random Access Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 297-313
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Optimal selection policies for a sequence of candidate drugs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 359-376
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Relating Time and Customer Averages for Queues Using ‘forward’ Coupling from the Past
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 568-574
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
A NOTE ON THE HU–HWANG–WANG CONJECTURE FOR GROUP TESTING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 561-571
-
- Article
-
- You have access
- Export citation
Transient Moments of the TCP Window Size Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 163-175
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Short-length routes in low-cost networks via Poisson line patterns
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-21
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The influence of dependence on data network models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 60-94
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Continuous Mixtures with Bathtub-Shaped Failure Rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 260-270
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
On the Structure of a Swing Contract's Optimal Value and Optimal Strategy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-15
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The Downtime Distribution After a Failure of a System with Multistate Independent Components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1068-1077
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Bounds for Owen's Multilinear Extension
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 852-864
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Optimal boarding policies for thin passengers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1098-1114
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
A Unifying Conservation Law for Single-Server Queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1078-1087
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Uniform renewal theory with applications to expansions of random geometric sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1070-1097
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Congestion-dependent pricing in a stochastic service system
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 898-921
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Explicit Gittins Indices for a Class of Superdiffusive Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 554-559
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
A Stochastic Ordering Property for Leaky Bucket Regulated Flows in Packet Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 332-348
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Large deviation properties of constant rate data streams sharing a buffer with long-range dependent traffic in critical loading
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 407-428
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Rendezvous Search with Revealed Information: Applications to the Line
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-15
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Optimal Control of a Large Dam
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 249-258
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
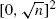 satisfying a weak equidistribution assumption. We show that if the first excess is
satisfying a weak equidistribution assumption. We show that if the first excess is