Refine listing
Actions for selected content:
556 results in 90Bxx
Utility Optimization in Congested Queueing Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 68-89
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Assessing the Reliability Function of Nanocomponents
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 31-42
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
On the Return Time for a Reflected Fractional Brownian Motion Process on the Positive Orthant
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 145-153
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
The asymptotic variance of departures in critically loaded queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 243-263
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Riemannian median and its estimation
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 December 2010, pp. 461-479
-
- Article
-
- You have access
- Export citation
Critical epidemics, random graphs, and Brownian motion with a parabolic drift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1187-1206
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Scaling limits for shortest path lengths along the edges of stationary tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 936-952
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Random Networks with Preferential Growth and Vertex Death
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1150-1163
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Probabilistic Analysis of the Efficacy of Periodic Testing of Employees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1174-1190
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Extreme value theory, Poisson-Dirichlet distributions, and first passage percolation on random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 706-738
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Limit theorems for random spatial drainage networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 659-688
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Interacting branching processes and linear file-sharing networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 834-854
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
A new look at transient versions of Little's law, and M/G/1 preemptive last-come-first-served queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 459-473
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
On reliability prediction and semi-renewal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 394-406
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Asymptotic analysis for personalized Web search
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 577-604
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Insensitive Bounds for the Moments of the Sojourn Times in M/GI Systems Under State-Dependent Processor Sharing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 246-267
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Optimal Control of a Stochastic Processing System Driven by a Fractional Brownian Motion Input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 183-209
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Generalized Measures of Divergence in Survival Analysis and Reliability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 216-234
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Optimal Allocation of Active Redundancies to k-out-of-n Systems with Heterogeneous Components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 254-263
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
On the Dual Relationship Between Markov Chains of GI/M/1 and M/G/1 Type
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 210-225
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
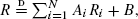 where the
where the 