Refine listing
Actions for selected content:
556 results in 90Bxx
On almost optimal priority rules for preemptive scheduling of stochastic jobs on parallel machines
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 821-839
- Print publication:
- September 1995
-
- Article
- Export citation
On M/G/1 queues with exhaustive service and generalized vacations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 510-531
- Print publication:
- June 1995
-
- Article
- Export citation
Product forms based on backward traffic equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 508-518
- Print publication:
- June 1995
-
- Article
- Export citation
A simple derivation of exact reliability formulas for linear and circular consecutive-k-of-n: F systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 554-557
- Print publication:
- June 1995
-
- Article
- Export citation
New partial ordering of survival functions based on the notion of uncertainty
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 202-211
- Print publication:
- March 1995
-
- Article
- Export citation
An optimal inspection–repair–replacement policy for standby systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 212-223
- Print publication:
- March 1995
-
- Article
- Export citation
The mean waiting time of a GI/G/1 queue in light traffic via random thinning
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 256-266
- Print publication:
- March 1995
-
- Article
- Export citation
Tight bounds on the sensitivity of generalised semi-Markov processes with a single generally distributed lifetime
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 63-73
- Print publication:
- March 1995
-
- Article
- Export citation
On redundancy allocations in systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1004-1014
- Print publication:
- December 1994
-
- Article
- Export citation
The departure process of the M/G/1 queueing model with server vacation and exhaustive service discipline
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1070-1082
- Print publication:
- December 1994
-
- Article
- Export citation
Some results on the relative ageing of two life distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 991-1003
- Print publication:
- December 1994
-
- Article
- Export citation
Servers in tandem with k-stage blocking and communications-type flow
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1061-1069
- Print publication:
- December 1994
-
- Article
- Export citation
A new approach to the G/G/1 queue with generalized setup time and exhaustive service
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1083-1097
- Print publication:
- December 1994
-
- Article
- Export citation
Approximations of large trunk line systems under heavy traffic
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1063-1094
- Print publication:
- December 1994
-
- Article
- Export citation
Exponential upper bounds via martingales for multiplexers with Markovian arrivals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1049-1060
- Print publication:
- December 1994
-
- Article
- Export citation
The optimality of LEPT in parallel machine scheduling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 788-796
- Print publication:
- September 1994
-
- Article
- Export citation
The Mk/G/∞ batch arrival queue by heterogeneous dependent demands
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 841-846
- Print publication:
- September 1994
-
- Article
- Export citation
Dynamic search for a moving target
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 438-457
- Print publication:
- June 1994
-
- Article
- Export citation
The Beňes equations for the distribution of excursions for general storage processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 418-429
- Print publication:
- June 1994
-
- Article
- Export citation
On the mean sojourn time of jobs in queues by general service disciplines
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 516-538
- Print publication:
- June 1994
-
- Article
- Export citation
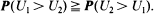 . Here we investigate the problem of allocating
. Here we investigate the problem of allocating 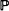 [queue length
[queue length 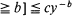 for any
for any 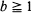 where
where 