In this paper we study scheduling problems of multiclass customers on identical parallel processors. A new type of arrival process, called a Markov decision arrival process, is introduced. This arrival process can be controlled and allows for an indirect dependence on the numbers of customers in the queues. As a special case we show the optimality of LEPT and the µc-rule in the last node of a controlled tandem network for various cost structures. A unifying proof using dynamic programming is given.

The main objective of this paper is to investigate the conditional behavior of the multivariate reward process given the number of certain signals where the underlying system is described by a semi-Markov process and the signal is defined by a counting process. To this end, we study the joint behavior of the multivariate reward process and the multivariate counting process in detail. We derive transform results as well as the corresponding real domain expressions, thus providing clear probabilistic interpretation.

The steady-state analysis of a quasi-birth-death process is possible by matrix geometric procedures in which the root to a quadratic matrix equation is found. A recent method that can be used for analyzing quasi-birth–death processes involves expanding the state space and using a linear matrix equation instead of the quadratic form. One of the difficulties of using the linear matrix equation approach regards the boundary conditions and obtaining the norming equation. In this paper, we present a method for calculating the boundary values and use the operator-machine interference problem as a vehicle to compare the two approaches for solving quasi-birth-death processes.

n unreliable machines are maintained by m repairmen. Assuming exponentially distributed up-time and repair time we find the optimal policy to allocate the repairmen to the failed machines in order to stochastically minimize the time until all machines work. Considering only one repairman, we find the optimal policy to maximize the expected total discount time that machines work. We find the optimal policy for the cases where the up-time and repair time are exponentially distributed or identically arbitrarily distributed up-times and increasing failure rate distribution repair times.

In this paper we present a simple combinatorial approach for the derivation of zero-avoiding transition probabilities in a Markovian r-node series Jackson network. The method we propose offers two advantages: first, it is conceptually simple because it is based on transition counts between the nodes and does not require a tensor representation of the network. Second, the method provides us with a very efficient technique for numerical computation of zero-avoiding transition probabilities.

For the original Moran dam with independent and identically distributed inputs a representation of the stationary distribution is given which readily provides a geometric rate of convergence to this distribution. For the integer-valued case the stationary distribution can be expressed in terms of simple boundary crossing probabilities for the underlying random walk.

We introduce and define for the first time the concept of a non-homogeneous Markov system in a stochastic environment (S-NHMS). The problem of finding the expected population structure in an S-NHMS is studied, and important properties among the basic parameters of the S-NHMS are established. Moreover, we study the problem of maintaining the relative sizes of the states in a stochastic environment applying control in the input process. Among other things, we provide the probability of maintaining any vector of relative state sizes. Also strategies for attaining in an optimal way a desired relative structure are designed, with the use of a given algorithm. Finally, an illustration is provided of the present results in a manpower system.

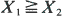Shanthikumar and Yao (1991) introduced some new stochastic order relations to compare the components of a bivariate random vector (X 1, X 2). As they point out in their paper, even if according to their hazard rate (or likelihood ratio) ordering, the marginal distributions may not be ordered accordingly. We introduce some new concepts where the marginal distributions preserve the corresponding stochastic orders. Also a relation between the bivariate scale model and the introduced bivariate hazard rate ordering is established.

An optimal allocation of subsystems depending on the system structure and reliability ordering of inherent subsystem components is determined, in the presence of various external influences on the reliability of components in different locations. It is carried out with the help of L-superadditive functions and Schur-convex functions.

Tandem queueing systems with blocking are frequently used in modelling of data communications and production transfer lines. We study such a system with no intermediate queues under the communication and the manufacturing blocking schemes and the assumption of just-in-time input. Explicit expressions for residence times, departure times, equilibrium throughput and some other measures of performance are obtained for the case of equal service requirements at all servers. This case is shown to be the ‘worst’ under the manufacturing blocking scheme, but not under the communication blocking scheme. An approximation formula is proposed for the equilibrium throughput in the case of exponential i.i.d. service times under the manufacturing blocking scheme.

A single machine is available to process a collection of stochastic jobs. Processing is preemptive and so (for example) the machine is allowed to switch away from a job before completion, should that prove advantageous. The jobs are deteriorating in the sense that their processing requirements grow (at job-specific rates) as they await processing. This phenomenon might be expected to enhance the status of non-preemptive policies. The primary objective of the paper is to find conditions which are sufficient to ensure the existence of a permutation policy to minimise the expected makespan. We also derive results for a weighted flowtime criterion. Applications of such models to the control of queues and to communication systems have been cited by other authors.

In this paper we introduce the concept of repair replacement. Repair replacement is a maintenance policy in which items are preventively maintained when a certain time has elapsed since their last repair. This differs from age replacement where a certain amount of time has elapsed since the last replacement. If the last repair was a complete repair, repair replacement is essentially the same as age replacement. It is in the case of minimal repair that these two policies differ. We make comparison between various types of policies in order to determine when and under which condition one type of policy is better than another.

We investigate the impact of switching penalties on the nature of optimal scheduling policies for systems of parallel queues without arrivals. We study two types of switching penalties incurred when switching between queues: lump sum costs and time delays. Under the assumption that the service periods of jobs in a given queue possess the same distribution, we derive an index rule that defines an optimal policy. For switching penalties that depend on the particular nodes involved in a switch, we show that although an index rule is not optimal in general, there is an exhaustive service policy that is optimal.

In flexible assembly systems, it is often necessary to coordinate jobs and materials so that specific jobs are matched with specific materials. This requires that jobs depart from upstream parallel workstations in some predetermined order. One way to satisfy this requirement is to temporarily hold the serviced jobs getting out of order at a resequencing buffer and to release them to downstream workstations as soon as all their predecessors are serviced. In this paper we consider the problem of scheduling a fixed number of non-preemptive jobs on two IHR non-identical processors with the resequencing requirement. We prove that the individually optimal policy, in which each job minimizes its own expected departure time subject to the constraint that available processors are offered to jobs in their departure order, is of a threshold type. The policy is independent of job weights and the jobs residing at the resequencing buffer and possesses the monotonicity property which states that a job will never utilize a processor in the future once it has declined the processor. Most importantly, we prove that the individually optimal policy has the stability property; namely: if at any time a job deviated from the individually optimal policy, then the departure time of every job, including its own, would be prolonged. As a direct consequence of this property, the individually optimal policy is socially optimal in the sense that it minimizes the expected total weighted departure time of the system as a whole. We identify situations under which the individually optimal policy also minimizes the expected makespan of the system.

In this paper we consider parallel and series systems, the components of which can be ‘improved'. The ‘improvement' consists of supplying the components with cold or hot standby spares or by allotting to them fixed budgets for minimal repairs. A fixed total resource of spares or minimal repairs is available. We find the optimal allocation of the resource items in several commonly encountered settings.

We provide a general framework for interconnecting a collection of quasi-reversible nodes in such a way that the resulting process exhibits a product-form invariant measure. The individual nodes can be quite general, although some degree of internal balance will be assumed. Any of the nodes may possess a feedback mechanism. Indeed, we pay particular attention to a class of feedback queues, characterized by the fact that their state description allows one to maintain a record of the order in which events occur. We also examine in some detail the problem of determining for which values of the arrival rates a node does exhibit quasi-reversibility.

We consider the class of bandit problems in which each of the n ≧ 2 independent arms generates rewards according to one of the same two reward distributions, and discounting is geometric over an infinite horizon. We show that the dynamic allocation index of Gittins and Jones (1974) in this context is strictly increasing in the probability that an arm is the better of the two distributions. It follows as an immediate consequence that myopic strategies are the uniquely optimal strategies in this class of bandit problems, regardless of the value of the discount parameter or the shape of the reward distributions. Some implications of this result for bandits with Bernoulli reward distributions are given.

Mathematical models have been proposed for oil exploration and other kinds of search. They can be used to estimate the amount of undiscovered resources or to investigate optimal stopping times for the search. Here we consider a continuous search for hidden objects using a model which represents the number and values of the objects by mixtures of Poisson processes. The flexibility of the model and its complexity depend on the number of components in the mixture. In simple cases, optimal stopping rules can be found explicitly and more general qualitative results can sometimes be obtained.

A single machine is available to process a collection of stochastic jobs preemptively. Rewards are received at job completions. We seek policies for machine allocation which maximize the total reward. Application areas point to the need to study such models for resource allocation when job processing requirements are dependent. To this end, models are developed in which the nature of such dependence is derived from various notions of positive and negative dependence in common usage in reliability. Optimal policies for resource allocation of simple structure are obtained for a variety of such models.

We consider scheduling problems with m machines in parallel and n jobs. The machines are subject to breakdown and repair. Jobs have exponentially distributed processing times and possibly random release dates. For cost functions that only depend on the set of uncompleted jobs at time t we provide necessary and sufficient conditions for the LEPT rule to minimize the expected cost at all t within the class of preemptive policies. This encompasses results that are known for makespan, and provides new results for the work remaining at time t. An application is that if the cµ rule has the same priority assignment as the LEPT rule then it minimizes the expected weighted number of jobs in the system for all t. Given appropriate conditions, we also show that the cµ rule minimizes the expected value of other objective functions, such as weighted sum of job completion times, weighted number of late jobs, or weighted sum of job tardinesses, when jobs have a common random due date.