We establish stability, monotonicity, concavity and subadditivity properties for open stochastic storage networks in which the driving process has stationary increments. A principal example is a stochastic fluid network in which the external inputs are random but all internal flows are deterministic. For the general model, the multi-dimensional content process is tight under the natural stability condition. The multi-dimensional content process is also stochastically increasing when the process starts at the origin, implying convergence to a proper limit under the natural stability condition. In addition, the content process is monotone in its initial conditions. Hence, when any content process with non-zero initial conditions hits the origin, it couples with the content process starting at the origin. However, in general, a tight content process need not hit the origin.

We consider the position of a tagged particle in the one-dimensional asymmetric nearest-neighbor simple exclusion process. Each particle attempts to jump to the site to its right at rate p and to the site to its left at rate q. The jump is realized if the destination site is empty. We assume p > q. The initial distribution is the product measure with density λ, conditioned to have a particle at the origin. We call X, the position at time t of this particle. Using a result recently proved by the authors for a semi-infinite zero-range process, it is shown that for all t ≧ 0, Xt = Nt − Bt + B 0 , where {N t} is a Poisson process of parameter (p – q)(1– λ) and {Bt } is a stationary process satisfying E exp (θ | B, |) < ∞ for some θ > 0. As a corollary we obtain that, properly centered and rescaled, the process {Xt } converges to Brownian motion. A previous result says that in the scale t 1/2, the position Xt is given by the initial number of empty sites in the interval (0, λt) divided by λ. We use this to compute the asymptotic covariance at time t of two tagged particles initially at sites 0 and rt. The results also hold for the net flux between two queues in a system of infinitely many queues in series.

We consider the machine repairman, or resource utilization, model in which there is a finite source of jobs with non-identically distributed exponential return times and a single server with job dependent service times. We also consider a related problem of scheduling jobs at heterogeneous servers. We construct a coupling framework that provides a simple unified proof that strengthens many of the results in the literature, and generalizes easily to prove several new results.

As a model for an ATM switch we consider the overflow frequency of a queue that is served at a constant rate and in which the arrival process is the superposition of N traffic streams. We consider an asymptotic as N → ∞ in which the service rate Nc and buffer size Nb also increase linearly in N. In this regime, the frequency of buffer overflow is approximately exp(–NI(c, b)), where I(c, b) is given by the solution to an optimization problem posed in terms of time-dependent logarithmic moment generating functions. Experimental results for Gaussian and Markov modulated fluid source models show that this asymptotic provides a better estimate of the frequency of buffer overflow than ones based on large buffer asymptotics.

We consider a stochastic fluid network with independent subordinator inputs to the various stations and deterministic internal flow which is of feed-forward type. We show that under suitable conditions the process of fluid contents in the station has a limiting distribution, where the limit holds in total variation and is independent of the initial condition. We also show that this limiting distribution is of product form only for trivial setups.

We study a model of a stochastic transportation system introduced by Crane. By adapting constructions of multidimensional reflected Brownian motion (RBM) that have since been developed for feedforward queueing networks, we generalize Crane's original functional central limit theorem results to a full vector setting, giving an explicit development for the case in which all terminals in the model experience heavy traffic conditions. We investigate product form conditions for the stationary distribution of our resulting RBM limit, and contrast our results for transportation networks with those for traditional queueing network models.

Vasicek (1977) proved that among all queueing disciplines that do not change the departure process of the queue, FIFO and LIFO yield, respectively, the smallest and the largest expectation of any given convex function of the service delay. In this note we further show that, if arriving customers join the queue stochastically ‘closer' to the server(s), then the expected value of any convex function of service delay is larger. As a more interesting result, we also show that if the function under consideration is concave, then the conclusion will be exactly the opposite. This result indicates that LIFO will be the best discipline if the delay cost is an increasing function but at a diminishing rate.

We explore a dynamic approach to the problems of call admission and resource allocation for communication networks with connections that are differentiated by their quality of service requirements. In a dynamic approach, the amount of spare resources is estimated on-line based on feedbacks from the network's quality of service monitoring mechanism. The schemes we propose remove the dependence on accurate traffic models and thus simplify the tasks of supplying traffic statistics required of network users. In this paper we present two dynamic algorithms. The objective of these algorithms is to find the minimum bandwidth necessary to satisfy a cell loss probability constraint at an asynchronous transfer mode (ATM) switch. We show that in both schemes the bandwidth chosen by the algorithm approaches the optimal value almost surely. Furthermore, in the second scheme, which determines the point closest to the optimal bandwidth from a finite number of choices, the expected learning time is finite.

This paper considers a modified block replacement with two variables and general random minimal repair cost. Under such a policy, an operating system is preventively replaced by new ones at times kT (k= 1, 2, ···) independently of its failure history. If the system fails in [(k − 1)T, (k − 1)T+ T0 ) it is either replaced by a new one or minimally repaired, and if in [(k − 1) T + T 0 , kT) it is either minimally repaired or remains inactive until the next planned replacement. The choice of these two possible actions is based on some random mechanism which is age-dependent. The cost of the ith minimal repair of the system at age y depends on the random part C(y) and the deterministic part ci (y). The expected cost rate is obtained, using the results of renewal reward theory. The model with two variables is transformed into a model with one variable and the optimum policy is discussed.

More applications of the principle for interchanging components due to Boland et al. (1989) in reliability theory are presented. In the context of active redundancy improvement we show that if two nodes are permutation equivalent then allocating a redundancy component to the weaker position always results in a larger increase in system reliability, which generalizes a previous result due to Boland et al. (1992). In the case of standby redundancy enhancement, we prove that a series (parallel) system is the only system for which standby redundancy at the component level is always more (less) effective than at the system level. Finally, the principle for interchanging components is extended from binary systems to the more complicated multistate systems.

In this paper we demonstrate that the distributional laws that relate the number of customers in the system (queue), L(Q) and the time a customer spends in the system (queue), S(W) under the first-in-first-out (FIFO) discipline are special cases of the H = λG law and lead to a complete solution for the distributions of L, Q, S, W for queueing systems which satisfy distributional laws for both L and Q (overtake free systems). Moreover, in such systems the derivation of the distributions of L, Q, S, W can be done in a unified way. Consequences of the distributional laws include a generalization of PASTA to queueing systems with arbitrary renewal arrivals under heavy traffic conditions, a generalization of the Pollaczek–Khinchine formula to the G//G/1 queue, an extension of the Fuhrmann and Cooper decomposition for queues with generalized vacations under mixed generalized Erlang renewal arrivals, approximate results for the distributions of L, S in a GI/G/∞ queue, and exact results for the distributions of L, Q, S, W in priority queues with mixed generalized Erlang renewal arrivals.

When analyzing the equilibrium behavior of M/G/1 type Markov chains by transform methods, restrictive hypotheses are often made to avoid technical problems that arise in applying results from complex analysis and linear algebra. It is shown that such restrictive assumptions are unnecessary, and an analysis of these chains using generating functions is given under only the natural hypotheses that first moments (or second moments in the null recurrent case) exist. The key to the analysis is the identification of an important subspace of the space of bounded solutions of the system of homogeneous vector-valued Wiener–Hopf equations associated with the chain. In particular, the linear equations in the boundary probabilities obtained from the transform method are shown to correspond to a spectral basis of the shift operator on this subspace. Necessary and sufficient conditions under which the chain is ergodic, null recurrent or transient are derived in terms of properties of the matrix-valued generating functions determined by transitions of the Markov chain. In the transient case, the Martin exit boundary is identified and shown to be associated with certain eigenvalues and vectors of one of these generating functions. An equilibrium analysis of the class of G/M/1 type Markov chains by similar methods is also presented.

In order to describe the evolution of the attainable structures of a continuous time homogeneous Markov system (HMS) with fixed size, we evaluate the volume of the sets of the attainable structures in Euclidean space in the course of time, and we find the value of the volume asymptotically. Then, using the concept of the volume of the attainable structures, we provide a method to evaluate the ‘age' of the system in continuous and discrete time. We also estimate the evolution of the distance of two (attainable) structures of the system as it changes following the transformations of the structures.

The comparison of optimal strategies in a simple stochastic replacement model for two types of machines with identical cost characteristics when one of them is more reliable than the other is conducted. It is proven that the scheduled replacement period for the more reliable type is always less than for the less reliable one. An example is presented when even the expected period of use of a more reliable machine is less than the expected period for the less reliable one. Some related problems are briefly discussed.

A queueing network with arbitrary topology, state dependent routing and flow control is considered. Customers may enter the network at any queue and they are routed through it until they reach certain queues from which they may leave the system. The routing is based on local state information. The service rate of a server is controlled based on local state information as well. A distributed policy for routing and service rate control is identified that achieves maximum throughput. The policy can be implemented without knowledge of the arrival and service rates. The importance of flow control is demonstrated by showing that, in certain networks, if the servers cannot be forced to idle, then no maximum throughput policy exists when the arrival rates are not known. Also a model for exchange of state information among neighboring nodes is presented and the network is studied when the routing is based on delayed state information. A distributed policy is shown to achieve maximum throughput in the case of delayed state information. Finally, some implications for deterministic flow networks are discussed.

We consider a non-Bayesian infinite horizon version of the multi-armed bandit problem with the objective of designing simple policies whose regret increases slowly with time. In their seminal work on this problem, Lai and Robbins had obtained a O(log n) lower bound on the regret with a constant that depends on the Kullback–Leibler number. They also constructed policies for some specific families of probability distributions (including exponential families) that achieved the lower bound. In this paper we construct index policies that depend on the rewards from each arm only through their sample mean. These policies are computationally much simpler and are also applicable much more generally. They achieve a O(log n) regret with a constant that is also based on the Kullback–Leibler number. This constant turns out to be optimal for one-parameter exponential families; however, in general it is derived from the optimal one via a ‘contraction' principle. Our results rely entirely on a few key lemmas from the theory of large deviations.

In this paper we consider a family of product-form loss models, including loss networks (or circuit-switched communication networks) and a class of resource-sharing models. There can be multiple classes of requests for multiple resources. Requests arrive according to independent Poisson processes. The requests can be for multiple units in each resource (the multi-rate case, e.g. several circuits on a trunk). There can be upper-limit and guaranteed-minimum sharing policies as well as the standard complete-sharing policy. If all the requirements of a request cannot be met upon arrival, then the request is blocked and lost. We develop an algorithm for computing the (exact) steady-state blocking probability of each class and other steady state descriptions in these loss models. The algorithm is based on numerically inverting generating functions of the normalization constants. In a previous paper we introduced this approach to product-form models and developed a full algorithm for a class of closed queueing networks. The inversion algorithm promises to be even more useful for loss models than for closed queueing networks because fewer alternative algorithms are available for loss models. Indeed, for many loss models with sharing policies other than traditional complete sharing, our algorithm is the first effective algorithm. Unlike some recursive algorithms, our algorithm has a low storage requirement. To treat the loss models here, we derive the generating functions of the normalization constants and develop a new scaling algorithm especially tailored to the loss models. In general, the computational complexity grows exponentially in the number of resources, but the computation can often be reduced dramatically by exploiting conditional decomposition based on special structure and by appropriately truncating large finite sums. We illustrate our numerical inversion algorithm by applying it to several examples. To validate our algorithm on small models, we also develop a direct algorithm. The direct algorithm itself is of interest, because it tends to be more efficient when the number of resources is large, but the number of request classes is small. Furthermore, it also allows a form of conditional decomposition based on special structure.

Formulas for the asymptotic failure rate, long-term average availability, and the limiting distribution of the number of long ‘outages' are obtained for a general class of two-state reliability models for maintained systems. The results extend known formulas for alternating renewal processes to a wider class of point processes that includes sequences of dependent or non-identically distributed operating and repair times.

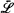Sharp upper and lower reliability bounds for the ℒ- and -classes of life distributions with a given mean are provided. Bounds are also given for a distribution which is related to a known distribution (not necessarily exponential) through the Laplace order.

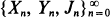A trivariate stochastic process is considered, describing a sequence of random shocks {Xn } at random intervals {Y n} with random system state {Jn }. The triviariate stochastic process satisfies a Markov renewal property in that the magnitude of shocks and the shock intervals are correlated pairwise and the corresponding joint distributions are affected by transitions of the system state which occur after each shock according to a Markov chain. Of interest is a system lifetime terminated whenever a shock magnitude exceeds a prespecified level z. The distribution of system lifetime, its moments and a related exponential limit theorem are derived explicitly. A similar transform analysis is conducted for a second type of system lifetime with system failures caused by the cumulative magnitude of shocks exceeding a fixed level z.