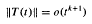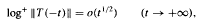Refine listing
Actions for selected content:
64 results in 47Dxx
Lp–Lrestimates for the Poisson semigroup on homogeneous trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 20-32
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
On improvements of the order of approximation in the Poisson limit theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 146-155
- Print publication:
- March 1996
-
- Article
- Export citation
Stationary distributions under mutation-selection balance: structure and properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 227-251
- Print publication:
- March 1996
-
- Article
- Export citation
Spectral synthesis and applications to C0-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 128-142
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
 be a homogeneous tree of degree at least three. In this paper we investigate for which values of
be a homogeneous tree of degree at least three. In this paper we investigate for which values of