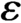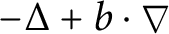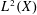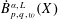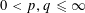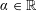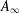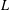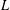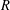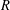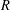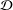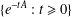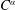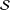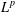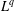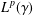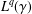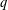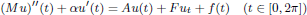Refine listing
Actions for selected content:
64 results in 47Dxx
The fragmentation equation with size diffusion: Well posedness and long-term behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 December 2021, pp. 1083-1116
-
- Article
- Export citation
TRANSITION DENSITIES OF SUBORDINATORS OF POSITIVE ORDER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 22 October 2021, pp. 1119-1179
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FUNCTIONAL CALCULI FOR SECTORIAL OPERATORS AND RELATED FUNCTION THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 04 October 2021, pp. 1383-1463
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wold decomposition on odometer semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 13 July 2021, pp. 738-755
- Print publication:
- June 2022
-
- Article
- Export citation
Noncommutative strong maximals and almost uniform convergence in several directions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e57
-
- Article
-
- You have access
- Open access
- Export citation
Regularity theory of Kolmogorov operator revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 24 August 2020, pp. 725-736
- Print publication:
- December 2021
-
- Article
- Export citation
Variation of constants formula and exponential dichotomy for nonautonomous non-densely defined Cauchy problems
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1347-1389
- Print publication:
- October 2021
-
- Article
- Export citation
WEIGHTED BESOV AND TRIEBEL–LIZORKIN SPACES ASSOCIATED WITH OPERATORS AND APPLICATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 February 2020, e11
-
- Article
-
- You have access
- Open access
- Export citation
POWERS OF COMPOSITION OPERATORS: ASYMPTOTIC BEHAVIOUR ON BERGMAN, DIRICHLET AND BLOCH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 289-320
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
NEW COUNTEREXAMPLES ON RITT OPERATORS, SECTORIAL OPERATORS AND
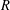 $R$-BOUNDEDNESS
$R$-BOUNDEDNESS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 11 April 2019, pp. 498-506
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Existence, Uniqueness and Qualitative Properties of Global Solutions of Abstract Differential Equations with State-Dependent Delay
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 771-788
-
- Article
- Export citation
Well-posedness of Third Order Differential Equations in Hölder Continuous Function Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 715-726
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
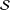 ${\mathcal{S}}$ -ASYMPTOTICALLY PERIODIC SOLUTIONS FOR ABSTRACT EQUATIONSWITH STATE-DEPENDENT DELAY
${\mathcal{S}}$ -ASYMPTOTICALLY PERIODIC SOLUTIONS FOR ABSTRACT EQUATIONSWITH STATE-DEPENDENT DELAY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 456-464
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Sobolev Algebras Through a ‘Carré Du Champ’ Identity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1041-1054
-
- Article
- Export citation
Intertwined Markov processes: the extended Chapman–Kolmogorov equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 123-131
- Print publication:
- February 2018
-
- Article
- Export citation
THE ROLE OF DOMINATION AND SMOOTHING CONDITIONS IN THE THEORY OF EVENTUALLY POSITIVE SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 286-298
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
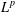 $L^{p}$ –
$L^{p}$ – 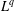 $L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS
$L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 154-161
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Well-Posedness of Second-Order Degenerate Differential Equations with Finite Delay
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 349-360
-
- Article
- Export citation
Well-posedness and regularity of linear hyperbolic systems with dynamic boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1047-1080
- Print publication:
- October 2016
-
- Article
- Export citation
SEMIGROUPS OF COMPOSITION OPERATORS ON LOCAL DIRICHLET SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 144-154
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation