Refine listing
Actions for selected content:
64 results in 47Dxx
The Growth Bound for Strongly Continuous Semigroups on Fréchet Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 23 November 2015, pp. 801-810
-
- Article
- Export citation
LEVEL SETS OF THE RESOLVENT NORM OF A LINEAR OPERATOR REVISITED
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 26 June 2015, pp. 243-265
- Print publication:
- 2016
-
- Article
- Export citation
SOME FELLER SEMIGROUPS ON
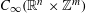 $C_{\infty }(\mathbb{R}^{n}\times \mathbb{Z}^{m})$ GENERATED BY PSEUDO-DIFFERENTIAL OPERATORS
$C_{\infty }(\mathbb{R}^{n}\times \mathbb{Z}^{m})$ GENERATED BY PSEUDO-DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 15 April 2015, pp. 402-413
- Print publication:
- May 2015
-
- Article
- Export citation
ON STABILITY OF SQUARE ROOT DOMAINS FOR NON-SELF-ADJOINT OPERATORS UNDER ADDITIVE PERTURBATIONS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 12 March 2015, pp. 111-182
- Print publication:
- 2016
-
- Article
- Export citation
ON COSINE FAMILIES CLOSE TO SCALAR COSINE FAMILIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 166-174
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
JOINS AND COVERS IN INVERSE SEMIGROUPS AND TIGHT
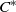 ${C}^{\ast } $-ALGEBRAS
${C}^{\ast } $-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 121-133
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Markov Processes with Restart
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 960-968
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Hitting Times, Occupation Times, Trivariate Laws and the Forward Kolmogorov Equation for a One-Dimensional Diffusion with Memory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 860-875
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
EXISTENCE RESULTS FOR A CLASS OF ABSTRACT IMPULSIVE DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 18 March 2013, pp. 366-385
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Laguerre semigroup and Dunkl operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 18 May 2012, pp. 1265-1336
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Convergence of Brownian motion with a scaled Dirac delta potential
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 403-427
-
- Article
-
- You have access
- Export citation
POINTWISE CONVERGENCE AND SEMIGROUPS ACTING ON VECTOR-VALUED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 22 March 2011, pp. 44-48
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
SMOOTH SOLUTIONS OF VOLTERRA EQUATIONS VIA SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 249-260
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
REMARKS ON ℓ1 AND
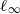 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 345-365
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
ON R-SECTORIAL DERIVATIVES ON BERGMAN SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 305-313
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
THE COMPLEX INVERSION FORMULA REVISITED
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-83
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Spectral and asymptotic properties of resolvent-dominated operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 181-201
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
Subordination in the sense of Bochner and a related functional calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 368-396
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Ergodicity and differences of functions on semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-265
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
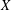
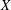
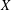

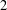

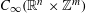
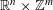
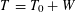
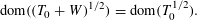
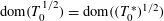
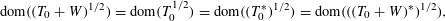
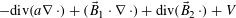
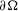
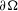
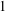
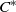
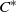
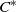
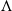
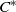
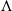
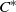
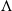
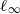 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
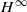 -calculus, and give a complete characterization of this condition in the case of Banach spaces which are
-calculus, and give a complete characterization of this condition in the case of Banach spaces which are 