Refine listing
Actions for selected content:
52 results in 78Axx
Numerical Simulations of Two Coaxial Vortex Rings Head-on Collision
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 616-647
- Print publication:
- August 2016
-
- Article
- Export citation
Analyses and Applications of the Second-Order Cross Correlation in the Passive Imaging
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1191-1220
- Print publication:
- May 2016
-
- Article
- Export citation
A Numerical Method on Eulerian Grids for Two-Phase Compressible Flow
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 187-212
- Print publication:
- April 2016
-
- Article
- Export citation
Integrating Feature Direction Information with a Level Set Formulation for Image Segmentation
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 1-22
- Print publication:
- February 2016
-
- Article
- Export citation
A Staggered Discontinuous Galerkin Method with Local TV Regularization for the Burgers Equation
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 451-474
- Print publication:
- November 2015
-
- Article
- Export citation
Efficient Operator Marching Method for Analyzing Crossed Arrays of Cylinders
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1461-1481
- Print publication:
- November 2015
-
- Article
- Export citation
Mathematical modelling of nano-scaled structures, devices and materials
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 347-348
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Electromagnetic wave propagation and inequalities for moments of chord lengths
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 987-995
- Print publication:
- December 2004
-
- Article
- Export citation
The evolution and measurement of a population of pairs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1048-1062
- Print publication:
- December 1995
-
- Article
- Export citation
The magnetic field perturbations produced by an ellipsoidal cavity in a uniform conductor
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 2 / December 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-255
- Print publication:
- December 1988
-
- Article
- Export citation
On a method of Fabrikant, Sankar and Swamy for a generalized potential problem
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 1 / June 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 72-86
- Print publication:
- June 1988
-
- Article
- Export citation
Three distribution identities and Maxwell's atomic field equations including the Röntgen current
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 240-246
- Print publication:
- December 1971
-
- Article
- Export citation
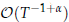 , with 0 <
, with 0 < 