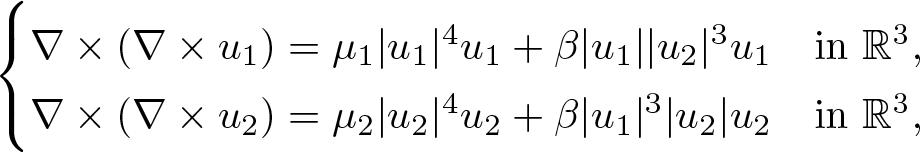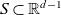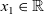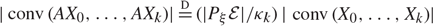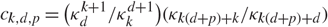Refine listing
Actions for selected content:
52 results in 78Axx
Travelling breather solutions in waveguides for cubic nonlinear Maxwell equations with retarded material laws
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 18 September 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ground state solution for weakly coupled time-harmonic Maxwell’s equations with critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 July 2025, pp. 1-31
-
- Article
- Export citation
DIFFRACTION OF THE PRIMES AND OTHER SETS OF ZERO DENSITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 202-245
- Print publication:
- October 2025
-
- Article
- Export citation
DETECTING MOISTURE IN BAUXITE USING MICROWAVES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 17 April 2024, pp. 308-346
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterising small objects in the regime between the eddy current model and wave propagation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 August 2023, pp. 294-317
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Increasing stability for the inverse source problem in elastic waves with attenuation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 896-910
-
- Article
- Export citation
A modelling framework for efficient reduced order simulations of parametrised lithium-ion battery cells
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 554-591
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectrum of weak model sets with Borel windows
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 June 2022, pp. 411-427
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inhomogeneous Helmholtz equations in wave guides – existence and uniqueness results with energy methods
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 March 2022, pp. 211-237
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Charge transport modelling of Lithium-ion batteries
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 21 October 2021, pp. 983-1031
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GEOMETRICALLY FLEXIBLE AND EFFICIENT NUMERICAL SOLUTION TECHNIQUE FOR BRAGG EDGE NEUTRON TRANSMISSION STRAIN TOMOGRAPHY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 12 August 2021, pp. 522-524
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
Understanding rapid charge and discharge in nano-structured lithium iron phosphate cathodes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 01 March 2021, pp. 328-368
-
- Article
-
- You have access
- Open access
- Export citation
Thin-layer solutions of the Helmholtz equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 769-783
-
- Article
- Export citation
Fano resonance in metallic grating via strongly coupled subwavelength resonators
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 30 June 2020, pp. 370-394
-
- Article
- Export citation
Random affine simplexes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 39-51
- Print publication:
- March 2019
-
- Article
- Export citation
WKB EXPANSIONS FOR HYPERBOLIC BOUNDARY VALUE PROBLEMS IN A STRIP: SELFINTERACTION MEETS STRONG WELL-POSEDNESS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1629-1675
- Print publication:
- September 2020
-
- Article
- Export citation
Asymptotic solutions of the Helmholtz equation: Generalised Friedlander–Keller ray expansions of fractional order
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 1-25
-
- Article
- Export citation
RECIPROCITY RELATIONS FOR A CONDUCTIVE SCATTERER WITH A CHIRAL CORE IN QUASI-STATIC FORM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 03 July 2018, pp. 86-94
-
- Article
-
- You have access
- Export citation
Rock Stress Around Noncircular Tunnel: a New Simple Mathematical Method
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1330-1346
- Print publication:
- December 2017
-
- Article
- Export citation
Convergence Analysis for the Chebyshev Collocation Methods to Volterra Integral Equations with a Weakly Singular Kernel
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1506-1524
- Print publication:
- December 2017
-
- Article
- Export citation