Refine listing
Actions for selected content:
33 results in 06Bxx
CHARACTERIZATION OF PROJECTIVE QUANTALES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 403-420
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
REGULAR CONGRUENCES ON AN IDEMPOTENT-REGULAR-SURJECTIVE SEMIGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 190-196
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
IRREDUCIBLE QUASIORDERS OF MONOUNARY ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 01 March 2013, pp. 259-276
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
VARIETIES WHOSE TOLERANCES ARE HOMOMORPHIC IMAGES OF THEIR CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 August 2012, pp. 326-338
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Quasi-Birth-and-Death Processes, Lattice Path Counting, and Hypergeometric Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-520
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
The Direct Decomposition of l-algebras into Products of Subdirectly Irreducible Factors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-56
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Congruence Representations of Join-homomorphisms of Finite Distributive Lattices: Size and Breadth
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-103
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
Covering in the lattice of subuniverses of a finite distributive lattice
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 333-353
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Maximal sublattices and Frattini sublattices of bounded lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 110-127
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Pasting infinite lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-21
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
A note on uniform ordered spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-352
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
Central relations on lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 3 / December 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-372
- Print publication:
- December 1983
-
- Article
-
- You have access
- Export citation
The lattice of stable marriages and permutations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 3 / December 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-410
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
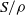
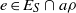
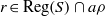
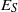
 (
(