Refine listing
Actions for selected content:
82 results in 34Kxx
Some comparison criteria in oscillation theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 2 / April 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 176-186
- Print publication:
- April 1984
-
- Article
-
- You have access
- Export citation
Some results on the asymptotic behavior of nonoscillatory solutions of differential equations with deviating arguments
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-317
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
-
This paper deals with some asymptotic properties of nonoscillatory solutions of a class of n-th order (n < 1) differential equations with deviationg arguments involving the so called n-th order r-derivative of the unknown function x defined by
where ri (i = 0,1…n) are positive continous functions on [t0, ∞). The fundamental purpose of this paper is to find for any integer m, 0 < m < n – 1, a necessary and sufficient condition (depending on m) in order that three exists at least one (nonoscillatory) solution x so that the
exists in R – {0} The results obtained extend some recent ones due to Philos (1978a) and they prove, in a general setting, the validity of a conjecture made by Kusano and Onose (1975).
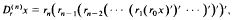
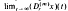exists in R – {0} The results obtained extend some recent ones due to Philos (1978a) and they prove, in a general setting, the validity of a conjecture made by Kusano and Onose (1975).