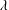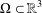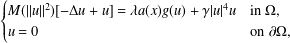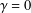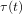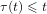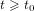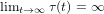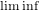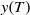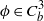Refine listing
Actions for selected content:
82 results in 34Kxx
Intra-specific competition and insect larval development: a model with time-dependent delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 353-369
- Print publication:
- April 2017
-
- Article
- Export citation
EXISTENCE OF POSITIVE SOLUTION FOR INDEFINITE KIRCHHOFF EQUATION IN EXTERIOR DOMAINS WITH SUBCRITICAL OR CRITICAL GROWTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 329-340
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
MOVING FRAMES AND NOETHER’S CONSERVATION LAWS—THE GENERAL CASE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 25 October 2016, e29
-
- Article
-
- You have access
- Open access
- Export citation
Well-Posedness of Second-Order Degenerate Differential Equations with Finite Delay
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 349-360
-
- Article
- Export citation
The moment exponential stability criterion of nonlinear hybrid stochastic differential equations and its discrete approximations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1303-1328
- Print publication:
- December 2016
-
- Article
- Export citation
Dependence Analysis of the Solutions on the Parameters of Fractional Neutral Delay Differential Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 772-783
- Print publication:
- October 2016
-
- Article
- Export citation
Oscillation of differential equations with non-monotone retarded arguments
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 98-104
-
- Article
-
- You have access
- Export citation
A CELL GROWTH MODEL ADAPTED FOR THE MINIMUM CELL SIZE DIVISION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 138-149
-
- Article
-
- You have access
- Export citation
Fitted Mesh Method for a Class of Singularly PerturbedDifferential-Difference Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 496-514
- Print publication:
- November 2015
-
- Article
- Export citation
The Runge–Kutta method in geometric multiplicative calculus
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 539-554
-
- Article
-
- You have access
- Export citation
WEIGHTED PSEUDO ALMOST PERIODIC SOLUTIONS FOR DIFFERENTIAL EQUATIONS WITH PIECEWISE CONSTANT ARGUMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 238-250
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
On Large Deviations for Small Noise Itô Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1126-1147
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
EFFECTS OF TIME DELAY ON THE DYNAMICS OF A KINETIC MODEL OF A MICROBIAL FERMENTATION PROCESS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. 336-356
-
- Article
-
- You have access
- Export citation
Optimal Stopping Problems in Diffusion-Type Models with Running Maxima and Drawdowns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 799-817
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
HOPF BIFURCATION ANALYSIS FOR A RATIO-DEPENDENT PREDATOR–PREY SYSTEM INVOLVING TWO DELAYS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 214-231
-
- Article
-
- You have access
- Export citation
ALMOST AUTOMORPHIC SOLUTIONS FOR DIFFERENTIAL EQUATIONS WITH PIECEWISE CONSTANT ARGUMENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 99-112
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Weak approximation of stochastic differential delay equations for bounded measurable function
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 September 2013, pp. 319-343
-
- Article
-
- You have access
- Export citation
CALCULUS FROM THE PAST: MULTIPLE DELAY SYSTEMS ARISING IN CANCER CELL MODELLING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 3 / January 2013
- Published online by Cambridge University Press:
- 30 April 2013, pp. 117-126
-
- Article
-
- You have access
- Export citation
EXISTENCE RESULTS FOR A CLASS OF ABSTRACT IMPULSIVE DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 18 March 2013, pp. 366-385
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Bayesian Quickest Detection Problems for Some Diffusion Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 164-185
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation