Refine listing
Actions for selected content:
82 results in 34Kxx
q-DISCRETE PAINLEVÉ EQUATIONS: THEIR HIERARCHIES AND PROPERTIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 14 September 2020, pp. 333-334
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
Transition waves for lattice Fisher-KPP equations with time and space dependence
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 April 2020, pp. 573-600
- Print publication:
- April 2021
-
- Article
- Export citation
Existence and stability of bistable wavefronts in a nonlocal delayed reaction–diffusion epidemic system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 146-176
-
- Article
- Export citation
Controllability of stochastic nonlinear oscillating delay systems driven by the Rosenblatt distribution
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 03 March 2020, pp. 217-239
- Print publication:
- February 2021
-
- Article
- Export citation
Stability of Almost Periodic Nicholson’s Blowflies Model Involving Patch Structure and Mortality Terms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 23 December 2019, pp. 405-422
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Existence and uniqueness of monotone wavefronts in a nonlocal resource-limited model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 2462-2483
- Print publication:
- October 2020
-
- Article
- Export citation
Existence, Uniqueness and Qualitative Properties of Global Solutions of Abstract Differential Equations with State-Dependent Delay
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 771-788
-
- Article
- Export citation
Existence of bistable waves for a nonlocal and nonmonotone reaction-diffusion equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 721-739
- Print publication:
- April 2020
-
- Article
- Export citation
Converge rates towards stationary solutions for the outflow problem of planar magnetohydrodynamics on a half line
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1291-1322
- Print publication:
- October 2019
-
- Article
- Export citation
QUANTITATIVE PROPERTIES OF MEROMORPHIC SOLUTIONS TO SOME DIFFERENTIAL-DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 250-261
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Well-posedness of Third Order Differential Equations in Hölder Continuous Function Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 715-726
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
On the stochastic resonance phenomenon in parametrically excited systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 26 September 2018, pp. 986-1003
-
- Article
- Export citation
Noise-induced mixing and multimodality in reaction networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 887-911
-
- Article
- Export citation
Approximate analytical solutions for a class of nonlinear stochastic differential equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 928-944
-
- Article
- Export citation
Positive periodic solutions for singular fourth-order differential equations with a deviating argument
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 10 May 2018, pp. 605-617
- Print publication:
- June 2018
-
- Article
- Export citation
Evaluating the Origin Intensity Factor in the Singular Boundary Method for Three-Dimensional Dirichlet Problems
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1289-1311
- Print publication:
- December 2017
-
- Article
- Export citation
SEMI-ANALYTICAL SOLUTIONS FOR THE BRUSSELATOR REACTION–DIFFUSION MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 October 2017, pp. 167-182
-
- Article
-
- You have access
- Export citation
Intertwined Markov processes: the extended Chapman–Kolmogorov equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 123-131
- Print publication:
- February 2018
-
- Article
- Export citation
Existence and properties of semi-bounded global solutions to the functional differential equation with Volterra-type operators on the real line
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1119-1168
- Print publication:
- December 2017
-
- Article
- Export citation
Treatment for third-order nonlinear differential equations based on the Adomian decomposition method
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 20 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 01 April 2017, pp. 1-10
-
- Article
-
- You have access
- Export citation
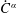
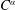
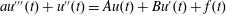
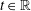
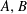
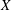
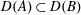
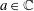
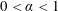
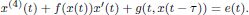
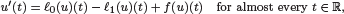
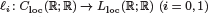 are linear positive continuous operators and
are linear positive continuous operators and 