Refine listing
Actions for selected content:
82 results in 34Kxx
Convexity-preserving flows of totally competitive planar Lotka–Volterra equations and the geometry of the carrying simplex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 53-63
-
- Article
-
- You have access
- Export citation
EIGENFUNCTIONS ARISING FROM A FIRST-ORDER FUNCTIONAL DIFFERENTIAL EQUATION IN A CELL GROWTH MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 1 / July 2010
- Published online by Cambridge University Press:
- 19 April 2011, pp. 46-58
-
- Article
-
- You have access
- Export citation
AN EIGENVALUE PROBLEM INVOLVING A FUNCTIONAL DIFFERENTIAL EQUATION ARISING IN A CELL GROWTH MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 4 / April 2010
- Published online by Cambridge University Press:
- 04 January 2011, pp. 383-393
-
- Article
-
- You have access
- Export citation
Projectors on the Generalized Eigenspaces for Neutral Functional Differential Equations in Lp Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-93
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
EXISTENCE RESULTS FOR ABSTRACT DEGENERATE NEUTRAL FUNCTIONAL DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 329-342
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
On the existence of positive solutions on the half-line to nonlinear two-dimensional delay differential systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 771-786
-
- Article
-
- You have access
- Export citation
STABILITY OF HALF-LINEAR NEUTRAL STOCHASTIC DIFFERENTIAL EQUATIONS WITH DELAYS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 13 August 2009, pp. 369-383
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
FURTHER RESULTS ON POSITIVE PERIODIC SOLUTIONS OF IMPULSIVE FUNCTIONAL DIFFERENTIAL EQUATIONS AND APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 27 July 2009, pp. 513-533
-
- Article
-
- You have access
- Export citation
Ricci iterations on Kähler classes
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 743-768
- Print publication:
- October 2009
-
- Article
- Export citation
EXISTENCE OF S-ASYMPTOTICALLY ω-PERIODIC SOLUTIONS FOR ABSTRACT NEUTRAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 365-382
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
DELAY-DEPENDENT ROBUST H∞ CONTROL FOR SINGULAR SYSTEMS WITH MULTIPLE DELAYS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 209-230
-
- Article
-
- You have access
- Export citation
THE BEST LEAST ABSOLUTE DEVIATIONS LINE – PROPERTIES AND TWO EFFICIENT METHODS FOR ITS DERIVATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 185-198
-
- Article
-
- You have access
- Export citation
NEW GRONWALL–OU-IANG TYPE INTEGRAL INEQUALITIES AND THEIR APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 111-127
-
- Article
-
- You have access
- Export citation
BOUNDEDNESS OF IMPULSIVE FUNCTIONAL DIFFERENTIAL EQUATIONS WITH VARIABLE IMPULSIVE PERTURBATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 331-345
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Discounted Optimal Stopping for Maxima of Some Jump-Diffusion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 713-731
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Ergodicity and stability of orbits of unbounded semigroup representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-232
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Existence and uniqueness for a class of mixed type differential equations
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 382-392
- Print publication:
- December 1996
-
- Article
- Export citation
Existence results for differential equations with reflection of the argument
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 237-260
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
Oscillations of higher order neutral differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 261-284
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
The delay differential equation
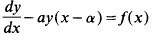
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 80-86
- Print publication:
- June 1986
-
- Article
- Export citation
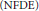
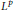
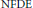
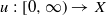 is said to be
is said to be 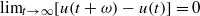 . This paper is devoted to study the existence and qualitative properties of
. This paper is devoted to study the existence and qualitative properties of 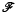 , the reduced Beurling spectrum of ø is empty if and only if ø ∈
, the reduced Beurling spectrum of ø is empty if and only if ø ∈ 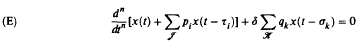
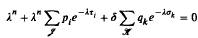
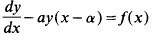
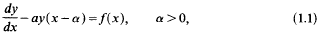
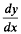 over 0 < x < α. As a result of integration, the value of
over 0 < x < α. As a result of integration, the value of 