Refine listing
Actions for selected content:
1705 results in 60Jxx
Asymptotic inference for nearly unstable INAR(1) models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 750-765
- Print publication:
- September 2003
-
- Article
- Export citation
On the entropy for semi-Markov processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1060-1068
- Print publication:
- September 2003
-
- Article
- Export citation
A note on quasi-stationary distributions of birth–death processes and the SIS logistic epidemic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 821-825
- Print publication:
- September 2003
-
- Article
- Export citation
Symmetric fixed points of a smoothing transformation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 377-394
- Print publication:
- June 2003
-
- Article
- Export citation
Zero-sum games for continuous-time Markov chains with unbounded transition and average payoff rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 327-345
- Print publication:
- June 2003
-
- Article
- Export citation
Stochastic ordering for continuous-time processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 361-375
- Print publication:
- June 2003
-
- Article
- Export citation
On the uniform ergodicity of Markov processes of order 2
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 455-472
- Print publication:
- June 2003
-
- Article
- Export citation
Discrete-time singularly perturbed Markov chains: aggregation, occupation measures, and switching diffusion limit
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 449-476
- Print publication:
- June 2003
-
- Article
- Export citation
Haplotypes: the joint distribution of alleles at linked loci
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 505-512
- Print publication:
- June 2003
-
- Article
- Export citation
On exact and large deviation approximation for the distribution of the longest run in a sequence of two-state Markov dependent trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 346-360
- Print publication:
- June 2003
-
- Article
- Export citation
Energy cascades as branching processes with emphasis on Neveu's approach to Derrida's random energy model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 477-503
- Print publication:
- June 2003
-
- Article
- Export citation
First passage times of a jump diffusion process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 504-531
- Print publication:
- June 2003
-
- Article
- Export citation
On Dufresne's relation between the probability laws of exponential functionals of Brownian motions with different drifts
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 184-206
- Print publication:
- March 2003
-
- Article
- Export citation
The coalescent process in a population with stochastically varying size
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 33-48
- Print publication:
- March 2003
-
- Article
- Export citation
Birth-death processes with an instantaneous reflection barrier
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 163-179
- Print publication:
- March 2003
-
- Article
- Export citation
On the N-tower problem and related problems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 278-294
- Print publication:
- March 2003
-
- Article
- Export citation
On the integral of the workload process of the single server queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 200-225
- Print publication:
- March 2003
-
- Article
- Export citation
On the integral of geometric Brownian motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 159-183
- Print publication:
- March 2003
-
- Article
- Export citation
Thick and thin points for random recursive fractals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 251-277
- Print publication:
- March 2003
-
- Article
- Export citation
Perturbed Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 107-122
- Print publication:
- March 2003
-
- Article
- Export citation
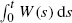 .
.