Refine listing
Actions for selected content:
1705 results in 60Jxx
Change-point models and conditionally pure birth processes: an inequality on the stochastic intensity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 939-952
- Print publication:
- December 2004
-
- Article
- Export citation
A continuous-time GARCH process driven by a Lévy process: stationarity and second-order behaviour
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 601-622
- Print publication:
- September 2004
-
- Article
- Export citation
The identifiability problem for repairable systems subject to competing risks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 774-790
- Print publication:
- September 2004
-
- Article
- Export citation
Telegraph processes with random velocities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 665-678
- Print publication:
- September 2004
-
- Article
- Export citation
A second-order Markov-modulated fluid queue with linear service rate
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 758-777
- Print publication:
- September 2004
-
- Article
- Export citation
Perturbation analysis for denumerable Markov chains with application to queueing models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 839-853
- Print publication:
- September 2004
-
- Article
- Export citation
Adaptive simulation using perfect control variates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 859-876
- Print publication:
- September 2004
-
- Article
- Export citation
Large deviations for supercritical multitype branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 703-720
- Print publication:
- September 2004
-
- Article
- Export citation
Ruin probabilities for competing claim processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 679-690
- Print publication:
- September 2004
-
- Article
- Export citation
Space filling and depletion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 691-702
- Print publication:
- September 2004
-
- Article
- Export citation
The log-normal approximation in financial and other computations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 747-773
- Print publication:
- September 2004
-
- Article
- Export citation
Recurrence properties of autoregressive processes with super-heavy-tailed innovations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 639-653
- Print publication:
- September 2004
-
- Article
- Export citation
Level-crossing probabilities and first-passage times for linear processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 643-666
- Print publication:
- June 2004
-
- Article
- Export citation
Limit theorem for continuous-time random walks with two time scales
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 455-466
- Print publication:
- June 2004
-
- Article
- Export citation
Measure change in multitype branching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 544-581
- Print publication:
- June 2004
-
- Article
- Export citation
Modelling the PCR amplification process by a size-dependent branching process and estimation of the efficiency
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 602-615
- Print publication:
- June 2004
-
- Article
- Export citation
Note on Zeifman's bounds on the rate of convergence for birth-death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 593-596
- Print publication:
- June 2004
-
- Article
- Export citation
Limit theorems for iterated random functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 425-436
- Print publication:
- June 2004
-
- Article
- Export citation
Convergence to the coalescent in populations of substantially varying size
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 368-378
- Print publication:
- June 2004
-
- Article
- Export citation
The compound Poisson immigration process subject to binomial catastrophes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 508-523
- Print publication:
- June 2004
-
- Article
- Export citation
 A similar estimator converges at rate
A similar estimator converges at rate 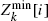 be the minimum possible population size at generation
be the minimum possible population size at generation 