We classify all (abstract) homomorphisms from the group $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\sf PGL}_{r+1}(\mathbf{C})$ to the group ${\sf Bir}(M)$ of birational transformations of a complex projective variety $M$, provided that $r\geq \dim _\mathbf{C}(M)$. As a byproduct, we show that: (i) ${\sf Bir}(\mathbb{P}^n_\mathbf{C})$ is isomorphic, as an abstract group, to ${\sf Bir}(\mathbb{P}^m_\mathbf{C})$ if and only if $n=m$; and (ii) $M$ is rational if and only if ${\sf PGL}_{\dim (M)+1}(\mathbf{C})$ embeds as a subgroup of ${\sf Bir}(M)$.

We show that the modulus of the Bergman kernel $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}B(z, \zeta )$ of a general homogeneous Siegel domain of type II is ‘almost constant’ uniformly with respect to $z$ when $\zeta $ varies inside a Bergman ball. The control is expressed in terms of the Bergman distance. This result was proved by A. Korányi for symmetric Siegel domains of type II. Subsequently, R. R. Coifman and R. Rochberg used it to establish an atomic decomposition theorem and an interpolation theorem by functions in Bergman spaces $A^p$ on these domains. The atomic decomposition theorem and the interpolation theorem are extended here to the general homogeneous case using the same tools. We further extend the range of exponents $p$ via functional analysis using recent estimates.

We prove that the Eisenstein–Picard modular group SU(2,1;ℤ[ω3]) can be generated by four given transformations.

In this paper we study the classification of holomorphic flows on Stein spaces of dimension two. We assume that the flow has periodic orbits, not necessarily with a same period. Then we prove a linearization result for the flow, under some natural conditions on the surface.

We study the boundedness properties of Rudin–Forelli-type operators associated to tubular domains over symmetric cones. As an application, we give a characterization of the topological dual space of the weighted Bergman space .

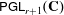
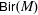
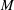
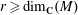
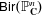
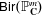
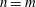
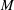
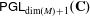
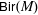
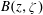
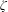
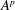
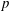
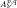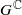We study the action of a real reductive group G on a real submanifold X of a Kähler manifold Z. We suppose that the action of G extends holomorphically to an action of the complexified group and that with respect to a compatible maximal compact subgroup 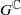U of the action on 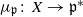Z is Hamiltonian. There is a corresponding gradient map where 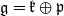is a Cartan decomposition of 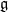. We obtain a Morse-like function 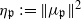on X. 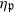Associated with critical points of are various sets of semistable points which we study in great detail. In particular, we have 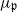G-stable submanifolds Sβ of X which are called pre-strata. In cases where is proper, the pre-strata form a decomposition of 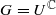X and in cases where X is compact they are the strata of a Morse-type stratification of X. Our results are generalizations of results of Kirwan obtained in the case where and X=Z is compact.