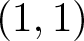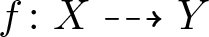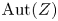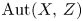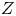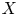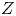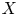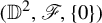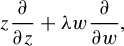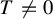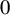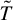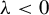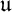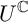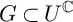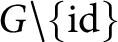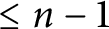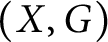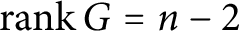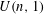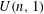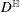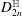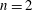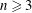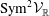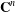Refine listing
Actions for selected content:
26 results in 32Nxx
Dynamics of generic automorphisms of Stein manifolds with the density property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 09 June 2025, pp. 3305-3324
- Print publication:
- November 2025
-
- Article
- Export citation
Invariant divisors and equivariant line bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rich representations and superrigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 2249-2272
- Print publication:
- August 2025
-
- Article
- Export citation
Moishezon manifolds with no nef and big classes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 198-204
-
- Article
- Export citation
A REMARK ON THE N-INVARIANT GEOMETRY OF BOUNDED HOMOGENEOUS DOMAINS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 23 May 2024, pp. 928-937
- Print publication:
- December 2024
-
- Article
- Export citation
Reversibility of affine transformations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 08 November 2023, pp. 1217-1228
-
- Article
- Export citation
CODIMENSION ONE FOLIATIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1705-1750
- Print publication:
- July 2024
-
- Article
- Export citation
A BALL QUOTIENT PARAMETRIZING TRIGONAL GENUS 4 CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 366-378
- Print publication:
- June 2024
-
- Article
- Export citation
Foliated affine and projective structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1153-1187
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARITHMETICITY OF
 $\mathbb {C}$-FUCHSIAN SUBGROUPS OF SOME NONARITHMETIC LATTICES
$\mathbb {C}$-FUCHSIAN SUBGROUPS OF SOME NONARITHMETIC LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 77-88
- Print publication:
- February 2024
-
- Article
- Export citation
Strongly Jordan property and free actions of non-abelian free groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 736-746
-
- Article
- Export citation
Directed harmonic currents near non-hyperbolic linearizable singularities
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 2228-2257
- Print publication:
- July 2023
-
- Article
- Export citation
COMPACT ORBITS OF PARABOLIC SUBGROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 14 December 2021, pp. 615-623
- Print publication:
- September 2022
-
- Article
- Export citation
Boundary maps and maximal representations on infinite-dimensional Hermitian symmetric spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 140-189
- Print publication:
- January 2023
-
- Article
- Export citation
Free abelian group actions on normal projective varieties: submaximal dynamical rank case
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 1057-1073
- Print publication:
- August 2021
-
- Article
- Export citation
HOMOGENEOUS SASAKI AND VAISMAN MANIFOLDS OF UNIMODULAR LIE GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 83-96
- Print publication:
- September 2021
-
- Article
- Export citation
ENDOSCOPY AND COHOMOLOGY IN A TOWER OF CONGRUENCE MANIFOLDS FOR
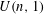 $U(n,1)$
$U(n,1)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 15 July 2019, e19
-
- Article
-
- You have access
- Open access
- Export citation
On Motivic Realizations of the Canonical Hermitian Variations of Hodge Structure of Calabi–Yau Type over type
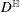 $D^{\mathbb{H}}$ Domains
$D^{\mathbb{H}}$ Domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 209-221
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
TAME DISCRETE SUBSETS IN STEIN MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 110-132
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Non-commutative automorphisms of bounded non-commutative domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 1037-1045
- Print publication:
- October 2016
-
- Article
- Export citation