Refine listing
Actions for selected content:
106 results in 62Hxx
Shape averages and their Bias
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 334-340
- Print publication:
- June 1994
-
- Article
- Export citation
Non-uniqueness in probabilistic numerical identification of bacteria
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 542-548
- Print publication:
- June 1994
-
- Article
- Export citation
Optimal second-order product probability bounds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 675-691
- Print publication:
- September 1993
-
- Article
- Export citation
Stochastic monotonicity and conditional Monte Carlo for likelihood ratios
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 103-115
- Print publication:
- March 1993
-
- Article
- Export citation
On the serial correlation for number in system in the stationary GI/M/1 bulk arrival and GI/Em /1 queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 404-417
- Print publication:
- June 1992
-
- Article
- Export citation
A Characterization and a Variational Inequality for the Multivariate Normal Distribution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-374
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
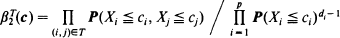
 alwayṡ dominates certain second-order Bonferroni bounds. Conditions on the covariance matrix of a N(0,Σ) distribution are given so that this bound applies, and various applications are given.
alwayṡ dominates certain second-order Bonferroni bounds. Conditions on the covariance matrix of a N(0,Σ) distribution are given so that this bound applies, and various applications are given.