Kohonen self-organizing interval maps are considered. In this model a linear graph is embedded randomly into the unit interval. At each time a point is chosen randomly according to a fixed distribution. The nearest vertex and some of its nearby neighbors are moved closer to the point. These models have been proposed as models of learning in the audio-cortex. The models possess not only the structure of a Markov chain, but also the added structure of a random dynamical system. This structure is used to show that for a large class of these models, in a strong way, the initial conditions are unimportant and only the dynamics govern the future. A contractive condition is proven in spite of the fact that the maps are not continuous. This, in turn, shows that the Markov chain is uniformly ergodic.

Techniques currently available in the literature in dealing with problems in geometric probabilities seem to rely heavily on results from differential and integral geometry. This paper provides a radical departure in this respect. By using purely algebraic procedures and making use of some properties of Jacobians of matrix transformations and functions of matrix argument, the distributional aspects of the random p-content of a p-parallelotope in Euclidean n-space are studied. The common assumptions of independence and rotational invariance of the random points are relaxed and the exact distributions and arbitrary moments, not just integer moments, are derived in this article. General real matrix-variate families of distributions, whose special cases include the mulivariate Gaussian, a multivariate type-1 beta, a multivariate type-2 beta and spherically symmetric distributions, are considered.

We exhibit solutions of Monge–Kantorovich mass transportation problems with constraints on the support of the feasible transportation plans and additional capacity restrictions. The Hoeffding–Fréchet inequalities are extended for bivariate distribution functions having fixed marginal distributions and satisfying additional constraints. Sharp bounds for different probabilistic functionals (e.g. Lp-distances, covariances, etc.) are given when the family of joint distribution functions has prescribed marginal distributions, satisfies restrictions on the support, and is bounded from above, or below, by other distributions.

For applications in spatial statistics, an important property of a random set X in ℝk is its first contact distribution. This is the distribution of the distance from a fixed point 0 to the nearest point of X, where distance is measured using scalar dilations of a fixed test set B. We show that, if B is convex and contains a neighbourhood of 0, the first contact distribution function FB is absolutely continuous. We give two explicit representations of FB, and additional regularity conditions under which FB is continuously differentiable. A Kaplan-Meier estimator of FB is introduced and its basic properties examined.

A stochastic dynamical context is developed for Bookstein's shape theory. It is shown how Bookstein's shape space for planar triangles arises naturally when the landmarks are moved around by a special Brownian motion on the general linear group of invertible (2×2) real matrices. Asymptotics for the Brownian transition density are used to suggest an exponential family of distributions, which is analogous to the von Mises-Fisher spherical distribution and which has already been studied by J. K. Jensen. The computer algebra implementation Itovsn3 (W. S. Kendall) of stochastic calculus is used to perform the calculations (some of which actually date back to work by Dyson on eigenvalues of random matrices and by Dynkin on Brownian motion on ellipsoids). An interesting feature of these calculations is that they include the first application (to the author's knowledge) of the Gröbner basis algorithm in a stochastic calculus context.

We consider the convex ordering for random vectors and some weaker versions of it, like the convex ordering for linear combinations of random variables. First we establish conditions of stochastic equality for random vectors that are ordered by one of the convex orderings. Then we establish necessary and sufficient conditions for the convex ordering to hold in the case of multivariate normal distributions and sufficient conditions for the positive linear convex ordering (without the restriction to multi-normality).

We present general criteria for analyzing the crossing characteristics of RI, the reliability function of an m-of-n system of components operating within a laboratory (or test-bench) environment, and RO, the reliability function of the same system now operating subject to an external environment. Inside the laboratory the components' lifetimes may be dependently distributed, and the external environment is modeled using the general approach of Lindley and Singpurwalla (1986). Our techniques, which utilize results basic to the theory of order statistics, apply to broad classes of external environment models.

We compare R1(t), the reliability function of a redundant m-of-n system operating within the laboratory, with RD(t), the reliability function of the same system operating subject to environmental effects. Within the laboratory, all component lifetimes are independent and identically distributed according to G(α + 1, λ), a gamma distribution with index α + 1 and scale λ. Outside the laboratory, we adopt the model of Lindley and Singpurwalla (J. Appl. Prob. 23 (1986), 418-431) and assume that, conditional on a positive random variable η which models the effect of the common environment, all component lifetimes are independent and identically distributed according to G(α + 1, λη). When α is a non-negative integer we prove that for RD(t) to underestimate (resp. overestimate) R1(t) for all t sufficiently close to zero, it is necessary and sufficient that E(η(n-m + 1)(α+1)) > 1 (resp. E(η(n-m + 1)(α+1)) < 1). In the case in which n = 2, m= 1 and α = 0 we obtain a special case of a result of Currit and Singpurwalla (J. Appl. Prob. 26 (1988), 763-771). As an application, we obtain a necessary and sufficient condition under which RD(t) initially understimates (or overestimates) R1(t) when η follows a gamma or an inverse Gaussian distribution.

A criterion is given for the existence of a stationary and causal multivariate integer-valued autoregressive process, MGINAR(p). The autocovariance function of this process being identical to the autocovariance function of a standard Gaussian MAR(p), we deduce that the MGINAR(p) process is nothing but a MAR(p) process. Consequently, the spectral density is directly found and gives good insight into the stochastic structure of a MGINAR(p). The estimation of parameters of the model, as well as the forecasting of the series, is discussed.

A characterization of the exponential distribution based on a relevation-type equation and its discrete version are extended to the case of multidimensional spaces via variants of the Choquet–Deny theorem. Comments on some recent results in the literature are made.

Conditions that have been widely used to establish stochastic ordering of random vectors include those given by Kamae et al. (1977), Barlow and Proschan (1975) and Langberg (1988). In this note we offer conditions that are weaker than those above, thus providing potential application to a wider class of problems.

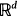The quadratic mean of the deviation between the probability content and the interior point proportion of a random convex hull in is investigated. We obtain, in particular, an explicit and distribution-independent bound.

A biphase image, representing the normal and degenerated fibres in a vertical cross-section of a nerve, is considered. A random set model based on a Gibbs point process is proposed for the union of the two phases. A kind of independence between the degeneration process and the original fibres is defined and tested.

Monotonicity and correlation results for queueing network processes, generalized birth–death processes and generalized migration processes are obtained with respect to various orderings of the state space. We prove positive (e.g. association) and negative (e.g. negative association) correlations in space and positive correlations in time for different situations, in steady state as well as in the transient phase of the system. This yields exact bounds for joint probabilities in terms of their independent versions.

In this paper we study the distribution associated with paired size-and-shape for two sets of correlated points having an underlying Gaussian distribution in the plane. This extends work previously done just for paired shape. Special cases are studied, and various properties described. In addition we give further results for the paired shape density.

The concept of max-infinite divisibility is viewed as a positive dependence concept. It is shown that every max-infinitely divisible distribution function is a multivariate totally positive function of order 2 (MTP2). Inequalities are derived, with emphasis on exchangeable distributions. Applications and examples are given throughout the paper.

The paper considers the bias of Bookstein's mean estimator for shape under the isotropic normal model. This work depends on certain distributional properties of shape variables. An alternative unbiased modified estimator is proposed and its performance is compared with various estimators, including Procrustes and the exact maximum likelihood estimator, in a simulation study.

In this note we point out an inherent difficulty in numerical identification of bacteria. The problem is that of uniqueness of the taxonomic structure or, in mathematical terms, the lack of statistical identifiability of finite mixtures of multivariate Bernoulli probability distributions shown here.

Let P(c) = P(X1 ≦ c1, · ··, Xp ≦ cp) for a random vector (X1, · ··, Xp). Bounds are considered of the form where T is a spanning tree corresponding to the bivariate probability structure and di is the degree of the vertex i in T. An optimized version of this inequality is obtained. The main result is that alwayṡ dominates certain second-order Bonferroni bounds. Conditions on the covariance matrix of a N(0,Σ) distribution are given so that this bound applies, and various applications are given.

Likelihood ratios are used in computer simulation to estimate expectations with respect to one law from simulation of another. This importance sampling technique can be implemented with either the likelihood ratio at the end of the simulated time horizon or with a sequence of likelihood ratios at intermediate times. Since a likelihood ratio process is a martingale, the intermediate values are conditional expectations of the final value and their use introduces no bias.

We provide conditions under which using conditional expectations in this way brings guaranteed variance reduction. We use stochastic orderings to get positive dependence between a process and its likelihood ratio, from which variance reduction follows. Our analysis supports the following rough statement: for increasing functionals of associated processes with monotone likelihood ratio, conditioning helps. Examples are drawn from recursively defined processes, Markov chains in discrete and continuous time, and processes with Poisson input.