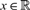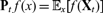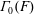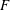Refine listing
Actions for selected content:
106 results in 62Hxx
On Tournaments and negative dependence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 February 2023, pp. 945-954
- Print publication:
- September 2023
-
- Article
- Export citation
CONVERGENCE RATE FOR STATISTICS OF POINT PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 28 September 2022, pp. 511-512
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
Gromov–Wasserstein distances between Gaussian distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1178-1198
- Print publication:
- December 2022
-
- Article
- Export citation
SPATIO-TEMPORAL MODELLING FOR NONSTATIONARY POINT REFERENCED DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 28 March 2022, pp. 518-519
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
DISTANCE MEASURES, INCONSISTENCY MATRICES AND ALGORITHMS FOR THE STUDY OF EPIDEMIOLOGICAL AND FINANCIAL CRISES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 January 2022, pp. 349-350
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
Sparse regular variation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1115-1148
- Print publication:
- December 2021
-
- Article
- Export citation
INFLUENCE FUNCTIONS FOR DIMENSION REDUCTION METHODS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 517-519
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
CONTRIBUTIONS TO ESTIMATION AND MODELING USING QUANTILES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 523-524
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
DEVELOPMENT OF MULTIVARIATE QUALITY CONTROL AND QUALITY ASSURANCE MODELS FOR ANTENATAL CARE SERVICE IN INDONESIA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 14 September 2020, pp. 346-348
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
Strong convergence of multivariate maxima
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 314-331
- Print publication:
- March 2020
-
- Article
- Export citation
Spectral projections correlation structure for short-to-long range dependent processes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 31 January 2020, pp. 1-31
-
- Article
- Export citation
THEORY AND STATISTICS OF LONG-RANGE DEPENDENT RANDOM PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 339-341
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
COPULA-BASED STATISTICAL MODELLING OF SYNOPTIC-SCALE CLIMATE INDICES FOR QUANTIFYING AND MANAGING AGRICULTURAL RISKS IN AUSTRALIA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 25 November 2019, pp. 166-169
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Stable Components and Layers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 562-576
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Conditional tail independence in Archimedean copula models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 858-869
- Print publication:
- September 2019
-
- Article
- Export citation
On a construction of multivariate distributions given some multidimensional marginals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 487-513
- Print publication:
- June 2019
-
- Article
- Export citation
Convergence rates for estimators of geodesic distances and Frèchet expectations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1001-1013
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
HOW FUNCTIONAL DATA CAN ENHANCE THE ESTIMATION OF HEALTH EXPECTANCY: THE CASE OF DISABLED SPANISH POPULATION
- Part of
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 49 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 22 November 2018, pp. 57-84
- Print publication:
- January 2019
-
- Article
- Export citation
On the consistency of the spacings test for multivariate uniformity, including on manifolds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 659-665
- Print publication:
- June 2018
-
- Article
- Export citation
Recovering a hidden community beyond the Kesten–Stigum threshold in O(|E|log*|V|) time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 325-352
- Print publication:
- June 2018
-
- Article
- Export citation