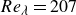Refine search
Actions for selected content:
237493 results in Physics and Astronomy
Small-scale dynamics and structure of free-surface turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 13 March 2025, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dedication
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp v-vi
-
- Chapter
- Export citation
Contents
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp vii-xii
-
- Chapter
- Export citation
2 - Discrete Events from Repeatability: “Quantum Jumps” and Wavepacket Collapse
- from Part I - Foundations
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp 17-43
-
- Chapter
- Export citation
1 - Introduction
- from Part I - Foundations
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp 3-16
-
- Chapter
- Export citation
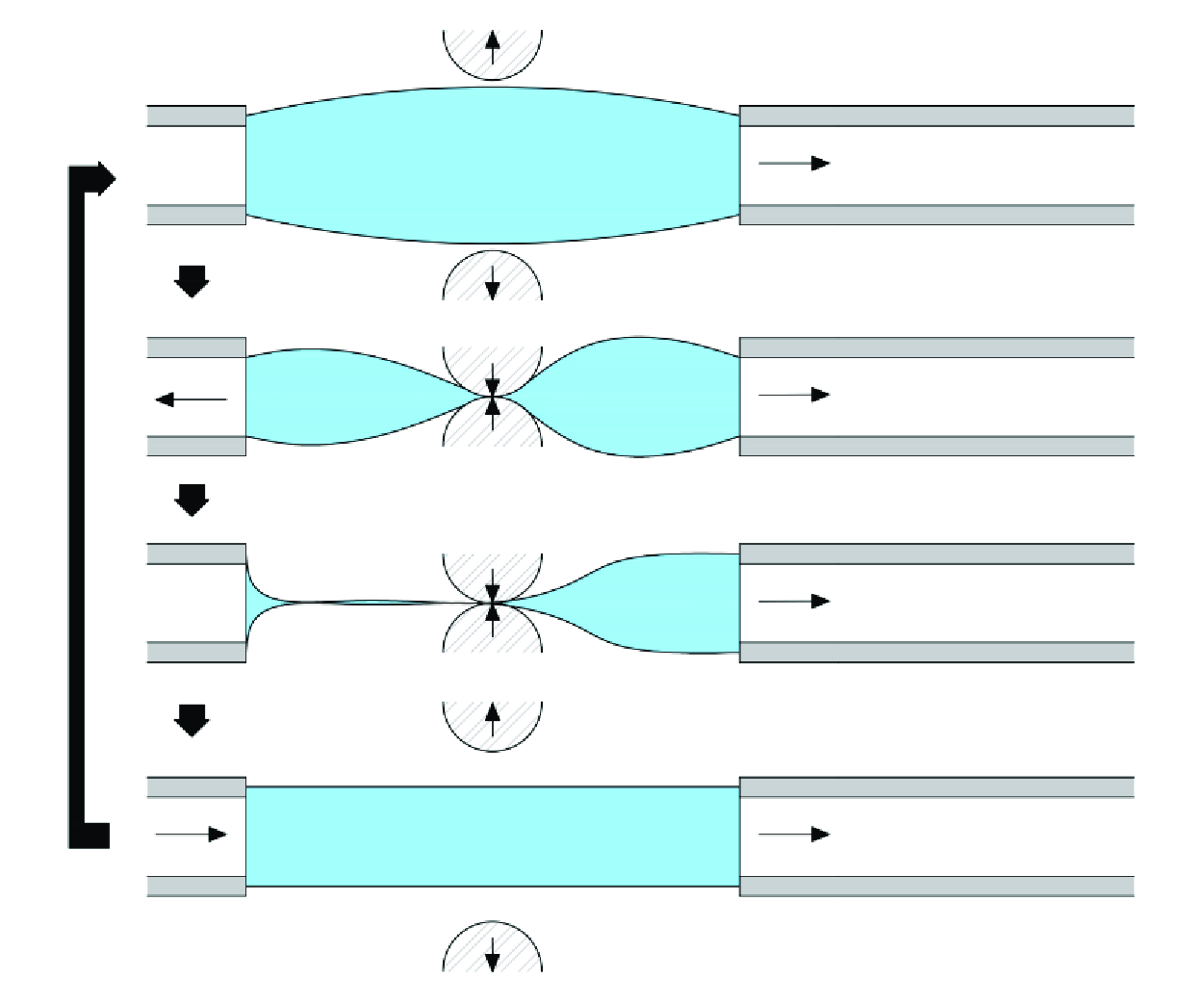
A semi-empirical model to predict resonant conditions in valveless asymmetric pumping
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 13 March 2025, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Born’s Rule from the Symmetries of Entanglement
- from Part I - Foundations
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp 44-74
-
- Chapter
- Export citation
Preface
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp xiii-xvii
-
- Chapter
- Export citation
9 - Quantum Darwinism and the Existential Interpretation
- from Part III - Quantum Darwinism
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp 262-335
-
- Chapter
- Export citation
Part III - Quantum Darwinism
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp 191-192
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Decoherence and Quantum Darwinism
- Published online:
- 06 March 2025
- Print publication:
- 13 March 2025, pp xviii-xviii
-
- Chapter
- Export citation
Self-similar flow of Newtonian and power-law viscous gravity currents in a confining gap in rectangular and axisymmetric geometries
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 12 March 2025, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unusual electron temperature profile due to grain electrostatics in planetary nebula cored dusty plasma
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 12 March 2025, E41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational methods for binding site prediction on macromolecules
-
- Journal:
- Quarterly Reviews of Biophysics / Volume 58 / 2025
- Published online by Cambridge University Press:
- 12 March 2025, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The role of an afterbody in flow-induced vibration of cylinders at low to moderate Reynolds numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 12 March 2025, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Particle-in-cell simulations of the tearing instability for relativistic pair plasmas
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 12 March 2025, E42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sensitivity of three-dimensional boundary layer stability to intrinsic uncertainties of fluid properties: a study on supercritical CO2
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 12 March 2025, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Magnetic reconnection, plasmoids and numerical resolution
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 12 March 2025, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dissipation in rapidly rotating fluid spheres caused by weak longitudinal libration
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 12 March 2025, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dispersive mixing: within or between pores?
-
- Journal:
- Journal of Fluid Mechanics / Volume 1006 / 10 March 2025
- Published online by Cambridge University Press:
- 12 March 2025, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation