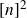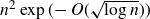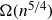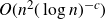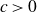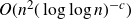Refine search
Actions for selected content:
237493 results in Physics and Astronomy
Improved bounds for skew corner-free sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 177-192
- Print publication:
- March 2025
-
- Article
- Export citation
PSP volume 178 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 24 April 2025, pp. f1-f2
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
The cokernel of a polynomial push-forward of a random integral matrix with concentrated residue
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 229-257
- Print publication:
- March 2025
-
- Article
- Export citation
Generating the liftable mapping class groups of regular cyclic covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 157-176
- Print publication:
- March 2025
-
- Article
- Export citation
Generalised Temperley–Lieb algebras of type G(r, p, n)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 193-227
- Print publication:
- March 2025
-
- Article
- Export citation
Stratified braid groups: monodromy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 259-292
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PSP volume 178 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 24 April 2025, pp. b1-b2
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
A scintillating fiber imaging spectrometer for active characterization of laser-driven proton beams – ERRATUM
-
- Journal:
- High Power Laser Science and Engineering / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 February 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gigahertz harmonic mode-locking with multi-watt sub-60-fs pulses in a Mamyshev oscillator
- Part of
-
- Journal:
- High Power Laser Science and Engineering / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 February 2025, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transition of solitary waves and undular bore from basin to channel with opposing current
- Part of
-
- Journal:
- Journal of Fluid Mechanics / Volume 1006 / 10 March 2025
- Published online by Cambridge University Press:
- 27 February 2025, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Passive spherical aberration compensation in laser diode side-pumped master oscillator power amplifier laser systems
-
- Journal:
- High Power Laser Science and Engineering / Volume 13 / 2025
- Published online by Cambridge University Press:
- 27 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coherent combining of large-aperture high-energy Nd:glass laser amplifiers
-
- Journal:
- High Power Laser Science and Engineering / Volume 13 / 2025
- Published online by Cambridge University Press:
- 27 February 2025, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Streamwise ram effect and tip vortex enhance the lift of a butterfly-inspired flapping wing
-
- Journal:
- Journal of Fluid Mechanics / Volume 1005 / 25 February 2025
- Published online by Cambridge University Press:
- 26 February 2025, A13
-
- Article
- Export citation
Liouville-type theorems for steady solutions to the Navier–Stokes system in a slab
-
- Journal:
- Journal of Fluid Mechanics / Volume 1005 / 25 February 2025
- Published online by Cambridge University Press:
- 26 February 2025, A6
-
- Article
- Export citation
Small-scale shear layers in isotropic turbulence of viscoelastic fluids
-
- Journal:
- Journal of Fluid Mechanics / Volume 1005 / 25 February 2025
- Published online by Cambridge University Press:
- 26 February 2025, A14
-
- Article
- Export citation
Plasma-based prism compressor design for high-intensity laser pulses
-
- Journal:
- High Power Laser Science and Engineering / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 February 2025, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Second-generation planet formation after tidal disruption from common envelope evolution
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 42 / 2025
- Published online by Cambridge University Press:
- 25 February 2025, e027
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Manipulating energy mergence of ultraintense femtosecond laser beamlets in underdense plasmas
-
- Journal:
- High Power Laser Science and Engineering / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 February 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Advanced plasma target from pre-ionized low-density foam for effective and robust direct laser acceleration of electrons
- Part of
-
- Journal:
- High Power Laser Science and Engineering / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 February 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scattering of surface waves by ocean currents: the U2H map
- Part of
-
- Journal:
- Journal of Fluid Mechanics / Volume 1005 / 25 February 2025
- Published online by Cambridge University Press:
- 24 February 2025, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation