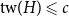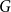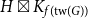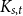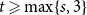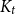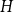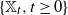Refine search
Actions for selected content:
52374 results in Statistics and Probability
Chapter Nine - The Role of Sampling in Inferential Statistics
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 270-288
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp iv-iv
-
- Chapter
- Export citation
Index
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 693-704
-
- Chapter
- Export citation
Chapter Three - Measures of Location, Spread, and Skewness
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 72-109
-
- Chapter
- Export citation
Chapter Nineteen - Accessing Data from Public-Use Sources
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 627-649
-
- Chapter
- Export citation
Contents
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp vii-xiv
-
- Chapter
- Export citation
Appendix C - Statistical Tables
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 666-687
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp xix-xx
-
- Chapter
- Export citation
Chapter Thirteen - One-Way Analysis of Variance
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 401-438
-
- Chapter
- Export citation
Product structure of graph classes with bounded treewidth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 December 2023, pp. 351-376
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter Sixteen - An Introduction To Multiple Regression
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 533-567
-
- Chapter
- Export citation
Chapter Eight - Theoretical Probability Models
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 243-269
-
- Chapter
- Export citation
Chapter Eighteen - Nonparametric Methods
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 595-626
-
- Chapter
- Export citation
Chapter Fourteen - Two-Way Analysis of Variance
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 439-483
-
- Chapter
- Export citation
Chapter Five - Exploring Relationships between Two Variables
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 148-194
-
- Chapter
- Export citation
Appendix B - .R Files and Datasets in R Format
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 665-665
-
- Chapter
- Export citation
Appendix D - Solutions TO END-OF-CHAPTER EXERCISES
-
- Book:
- Statistics Using R
- Published online:
- 07 December 2023
- Print publication:
- 07 December 2023, pp 688-688
-
- Chapter
- Export citation
ACCI could be a poor prognostic indicator for the in-hospital mortality of patients with SFTS
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 06 December 2023, e203
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak convergence of the extremes of branching Lévy processes with regularly varying tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 December 2023, pp. 622-643
- Print publication:
- June 2024
-
- Article
- Export citation
High prevalence of asymptomatic malaria in Forest Guinea: Results from a rapid community survey
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 05 December 2023, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation