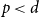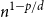Refine search
Actions for selected content:
52374 results in Statistics and Probability
3 - Estimation and Decision-Making
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 73-120
-
- Chapter
- Export citation
Appendices
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 707-745
-
- Chapter
- Export citation
On minimum spanning trees for random Euclidean bipartite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 319-350
-
- Article
- Export citation
8 - Spectral Analysis of Time Series
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 287-328
-
- Chapter
- Export citation
Preface
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp xv-xviii
-
- Chapter
- Export citation
6 - Covariance Matrices, EOFs, and PCs
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 200-242
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp xix-xx
-
- Chapter
- Export citation
Chapter Four - Re-expressing Variables
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 119-158
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp xix-xix
-
- Chapter
- Export citation
Chapter Ten - Inferences Involving the Mean of a Single Population when σ is Known
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 294-321
-
- Chapter
- Export citation
1 - Basics of Climate Data Arrays, Statistics, and Visualization
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 1-34
-
- Chapter
-
- You have access
- Export citation
Chapter Nineteen - Customizing and Exporting Tables to Microsoft Word and Excel Using the New Table Command
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 660-691
-
- Chapter
- Export citation
Dynamics of information networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 1029-1039
- Print publication:
- September 2024
-
- Article
- Export citation
Chapter Thirteen - One-Way Analysis of Variance
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 416-460
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp iv-iv
-
- Chapter
- Export citation
Chapter Fifteen - Correlation and Simple Regression as Inferential Techniques
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 507-556
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp i-iv
-
- Chapter
- Export citation
Chapter Fourteen - Two-Way Analysis of Variance
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 461-506
-
- Chapter
- Export citation
References
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 746-749
-
- Chapter
- Export citation
Chapter Eleven - Inferences Involving the Mean when σ is Not Known: One- and Two-Sample Designs
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 322-394
-
- Chapter
- Export citation