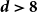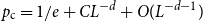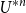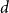Refine search
Actions for selected content:
52379 results in Statistics and Probability
Acknowledgments
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp xv-xvi
-
- Chapter
- Export citation
Chapter 5 - Benford Agreement Analysis of the Sea Around Us Project’s Fish-Landings Data
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 94-130
-
- Chapter
- Export citation
Chapter 4 - Data Characteristics and the Workflow of Benford Agreement Analysis
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 74-93
-
- Chapter
- Export citation
Chapter 7 - Assessing the Impacts of Problematic Benford Validity
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 169-187
-
- Chapter
- Export citation
Index
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 204-208
-
- Chapter
- Export citation
Chapter 3 - Benford’s Law and Assessing Conformity
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 24-73
-
- Chapter
- Export citation
Preface
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp xiii-xiv
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp iv-iv
-
- Chapter
- Export citation
Chapter 6 - Benford Agreement Analysis of US and Global COVID-19 New Cases Data
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 131-168
-
- Chapter
- Export citation
References
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 196-203
-
- Chapter
- Export citation
Tables
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp ix-xii
-
- Chapter
- Export citation
Chapter 1 - Introduction
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 1-10
-
- Chapter
- Export citation
Contents
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp v-vi
-
- Chapter
- Export citation
Chapter 2 - Validity and Self-Reported Data
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 11-23
-
- Chapter
- Export citation
Chapter 8 - Conclusion
-
- Book:
- Applying Benford's Law for Assessing the Validity of Social Science Data
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 188-195
-
- Chapter
- Export citation
Spread-out limit of the critical points for lattice trees and lattice animals in dimensions
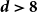 $\boldsymbol{d}\boldsymbol\gt \textbf{8}$
$\boldsymbol{d}\boldsymbol\gt \textbf{8}$
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 20 November 2023, pp. 238-269
-
- Article
- Export citation
SUBGEOMETRICALLY ERGODIC AUTOREGRESSIONS WITH AUTOREGRESSIVE CONDITIONAL HETEROSKEDASTICITY
-
- Journal:
- Econometric Theory / Volume 41 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 17 November 2023, pp. 218-248
-
- Article
- Export citation
A comparative analysis of public transport accessibility to hospitals in Córdoba (2019–2023): Where are we now?
-
- Journal:
- Data & Policy / Volume 5 / 2023
- Published online by Cambridge University Press:
- 17 November 2023, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal performance of a tontine overlay subject to withdrawal constraints
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 54 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 17 November 2023, pp. 94-128
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Frontmatter
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp i-vi
-
- Chapter
- Export citation