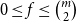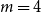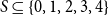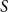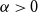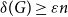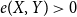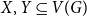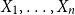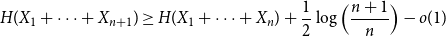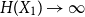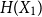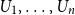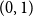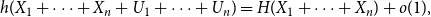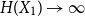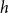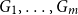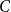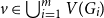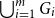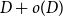Refine search
Actions for selected content:
52379 results in Statistics and Probability
8 - Interactions and Dichotomous Dependent Variables
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 315-400
-
- Chapter
- Export citation
6 - When We Have More Than One Modifying Variable
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 195-272
-
- Chapter
- Export citation
Appendix C - Calculating the Smallest Standard Error for the Marginal Effect of X on Y
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 498-499
-
- Chapter
- Export citation
5 - Three Substantive Applications
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 126-192
-
- Chapter
- Export citation
7 - When an Independent Variable Interacts with Itself
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 273-312
-
- Chapter
- Export citation
Large cliques or cocliques in hypergraphs with forbidden order-size pairs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 286-299
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Part II - More Complex Forms of Conditionality
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 193-194
-
- Chapter
- Export citation
Dedication
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp vii-viii
-
- Chapter
- Export citation
Injection drug use and sexually transmitted infections among men who have sex with men: A retrospective cohort study at an HIV/AIDS referral hospital in Tokyo, 2013–2022
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 15 November 2023, e195
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Seroprevalence of Zika in Brazil stratified by age and geographic distribution
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 15 November 2023, e197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spanning trees in graphs without large bipartite holes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 270-285
-
- Article
-
- You have access
- HTML
- Export citation
Approximate discrete entropy monotonicity for log-concave sums
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 196-209
-
- Article
- Export citation
Evaluation of phase-adjusted interventions for COVID-19 using an improved SEIR model
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 13 November 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Calibration of transition risk for corporate bonds
-
- Journal:
- British Actuarial Journal / Volume 28 / 2023
- Published online by Cambridge University Press:
- 13 November 2023, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prevalence and incidence of emergency department presentations and hospital separations with injecting-related infections in a longitudinal cohort of people who inject drugs
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 13 November 2023, e192
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Association between face mask use and risk of SARS-CoV-2 infection: Cross-sectional study
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 13 November 2023, e194
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERFORMANCE OF EMPIRICAL RISK MINIMIZATION FOR LINEAR REGRESSION WITH DEPENDENT DATA
-
- Journal:
- Econometric Theory / Volume 41 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 10 November 2023, pp. 391-420
-
- Article
-
- You have access
- Open access
- Export citation
A special case of Vu’s conjecture: colouring nearly disjoint graphs of bounded maximum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 179-195
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Statistics and Data Visualization in Climate Science with R and Python
-
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023

Applying Benford's Law for Assessing the Validity of Social Science Data
-
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023