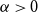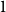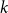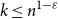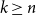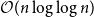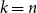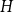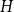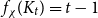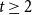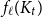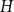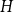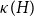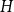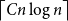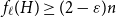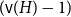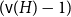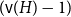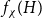Refine search
Actions for selected content:
52379 results in Statistics and Probability
Part II - Global Perspectives on Key Methods/Topics
-
- Book:
- Technology and Measurement around the Globe
- Published online:
- 08 November 2023
- Print publication:
- 09 November 2023, pp 129-210
-
- Chapter
- Export citation

Technology and Measurement around the Globe
-
- Published online:
- 08 November 2023
- Print publication:
- 09 November 2023
On oriented cycles in randomly perturbed digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 157-178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mastermind with a linear number of queries
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 143-156
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characteristics of the switch process and geometric divisibility
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 802-809
- Print publication:
- September 2024
-
- Article
- Export citation
Graph-based methods for discrete choice
-
- Journal:
- Network Science / Volume 12 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 21-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skin and soft tissue infection incidence before and during the COVID-19 pandemic
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 06 November 2023, e190
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUBSAMPLING INFERENCE FOR NONPARAMETRIC EXTREMAL CONDITIONAL QUANTILES
-
- Journal:
- Econometric Theory / Volume 41 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 06 November 2023, pp. 326-340
-
- Article
-
- You have access
- Open access
- Export citation
On the choosability of
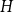 $H$-minor-free graphs
$H$-minor-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 129-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parametrized polyconvex hyperelasticity with physics-augmented neural networks
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 03 November 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Determinants of incomplete childhood hepatitis B vaccination in Sierra Leone, Liberia, and Guinea: Analysis of national surveys (2018–2020)
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 03 November 2023, e193
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding data science innovations in organizations: a new workflow approach
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 03 November 2023, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Incomplete to complete multiphysics forecasting: a hybrid approach for learning unknown phenomena
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 03 November 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Interaction Models
- Specification and Interpretation
-
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023
Tessellation-valued processes that are generated by cell division
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 November 2023, pp. 697-715
- Print publication:
- June 2024
-
- Article
- Export citation
Risk of severe outcomes among Omicron sub-lineages BA.4.6, BA.2.75, and BQ.1 compared to BA.5 in England
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 31 October 2023, e189
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trajectory fitting estimation for reflected stochastic linear differential equations of a large signal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 741-754
- Print publication:
- September 2024
-
- Article
- Export citation
Capital requirement modeling for market and non-life premium risk in a dynamic insurance portfolio
-
- Journal:
- Annals of Actuarial Science / Volume 18 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 205-236
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A large-deviation principle for birth–death processes with a linear rate of downward jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 781-801
- Print publication:
- September 2024
-
- Article
- Export citation
COVID-19 epidemiology and rural healthcare: a survey in a Spanish village
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 27 October 2023, e188
-
- Article
-
- You have access
- Open access
- HTML
- Export citation