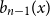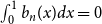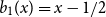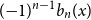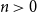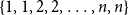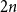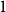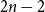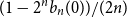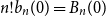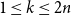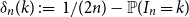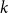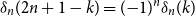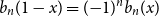Refine search
Actions for selected content:
52379 results in Statistics and Probability
References
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 506-523
-
- Chapter
- Export citation
10 - Interactions and Unordered Dependent Variables
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 433-492
-
- Chapter
- Export citation
Figures
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp xiii-xvii
-
- Chapter
- Export citation
Appendix A - Basic Properties of Variances
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 493-494
-
- Chapter
- Export citation
Tables
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp xviii-xx
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 1-12
-
- Chapter
- Export citation
Appendix D - Calculating the Values of the Modifying Variable Z at which the Bounds of the Confidence Interval for the Marginal Effect of X Equal 0
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 500-505
-
- Chapter
- Export citation
Solutions
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 524-577
-
- Chapter
- Export citation
The Bernoulli clock: probabilistic and combinatorial interpretations of the Bernoulli polynomials by circular convolution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 210-237
-
- Article
- Export citation
Appendix B - Marginal Effects and Variances for Various Linear-Interactive Models
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 495-497
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp xxvii-xxviii
-
- Chapter
- Export citation
Part I - The Fundamentals
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 13-14
-
- Chapter
- Export citation
Alphabetical Index
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 578-584
-
- Chapter
- Export citation
3 - Interaction Model Specification
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 53-97
-
- Chapter
- Export citation
Contents
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp ix-xii
-
- Chapter
- Export citation
Preface
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp xxi-xxvi
-
- Chapter
- Export citation
9 - Interactions and Ordered Dependent Variables
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 401-432
-
- Chapter
- Export citation
4 - Interpreting Quantities of Interest
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 98-125
-
- Chapter
- Export citation
Part III - Interactions and Limited Dependent Variables
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 313-314
-
- Chapter
- Export citation
2 - Theories and Their Conditional Implications
-
- Book:
- Interaction Models
- Published online:
- 02 November 2023
- Print publication:
- 16 November 2023, pp 15-52
-
- Chapter
- Export citation