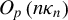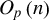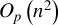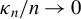Refine search
Actions for selected content:
52382 results in Statistics and Probability
Index
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 687-690
-
- Chapter
- Export citation
References
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 667-682
-
- Chapter
- Export citation
Contents
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp vii-x
-
- Chapter
- Export citation
5 - Linear Nonparametric Estimators
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 389-466
-
- Chapter
- Export citation
Epidemiological analysis of a COVID-19 outbreak associated with an infected surgeon
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 25 March 2021, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A simple model for the total number of SARS-CoV-2 infections on a national level
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 25 March 2021, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Preface
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp xi-xiv
-
- Chapter
- Export citation
7 - Likelihood-Based Procedures
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 541-606
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp i-iv
-
- Chapter
- Export citation
8 - Adaptive Inference
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 607-666
-
- Chapter
- Export citation
Dedication
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp v-vi
-
- Chapter
- Export citation
2 - Gaussian Processes
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 15-108
-
- Chapter
- Export citation
Author Index
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 683-686
-
- Chapter
- Export citation
1 - Nonparametric Statistical Models
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 1-14
-
- Chapter
- Export citation
6 - The Minimax Paradigm
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 467-540
-
- Chapter
- Export citation
3 - Empirical Processes
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 109-290
-
- Chapter
- Export citation
4 - Function Spaces and Approximation Theory
-
- Book:
- Mathematical Foundations of Infinite-Dimensional Statistical Models
- Published online:
- 05 March 2021
- Print publication:
- 25 March 2021, pp 291-388
-
- Chapter
- Export citation
SEQUENTIAL MONITORING OF CHANGES IN DYNAMIC LINEAR MODELS, APPLIED TO THE U.S. HOUSING MARKET
-
- Journal:
- Econometric Theory / Volume 38 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 209-272
-
- Article
- Export citation
Powers of paths in tournaments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 23 March 2021, pp. 894-898
-
- Article
- Export citation
LEAST SQUARES AND IVX LIMIT THEORY IN SYSTEMS OF PREDICTIVE REGRESSIONS WITH GARCH INNOVATIONS
-
- Journal:
- Econometric Theory / Volume 38 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 875-912
-
- Article
- Export citation
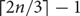 , which is best possible.
, which is best possible.