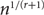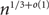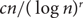Refine search
Actions for selected content:
52383 results in Statistics and Probability
Appendix B - .R Files and Datasets in R Format
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp 641-641
-
- Chapter
- Export citation
16 - An Introduction To Multiple Regression
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp 531-565
-
- Chapter
- Export citation
17 - Two-Way Interactions In Multiple Regression
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp 566-592
-
- Chapter
- Export citation
11 - Inferences Involving The Mean When σ Is Not Known: One- And Two-Sample Designs
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp 316-377
-
- Chapter
- Export citation
10 - Inferences Involving The Mean Of a Single Population When σ is Known
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp 287-315
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp xviii-xviii
-
- Chapter
- Export citation
Improved Ramsey-type results for comparability graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 13 August 2020, pp. 747-756
-
- Article
- Export citation
Preface
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp xv-xvii
-
- Chapter
- Export citation
7 - Probability Fundamentals
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp 221-241
-
- Chapter
- Export citation
3 - Measures Of Location, Spread, And Skewness
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp 70-107
-
- Chapter
- Export citation
9 - The Role Of Sampling In Inferential Statistics
-
- Book:
- Statistics Using R
- Published online:
- 23 September 2020
- Print publication:
- 13 August 2020, pp 268-286
-
- Chapter
- Export citation
PES volume 34 issue 3 Cover and Back matter
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 3 / July 2020
- Published online by Cambridge University Press:
- 12 August 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Capsular polysaccharide and lipopolysaccharide O type analysis of Klebsiella pneumoniae isolates by genotype in China
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 12 August 2020, e191
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PES volume 34 issue 3 Cover and Front matter
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 3 / July 2020
- Published online by Cambridge University Press:
- 12 August 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Robustness of randomized rumour spreading
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 August 2020, pp. 37-78
-
- Article
-
- You have access
- Open access
- Export citation
Risk factors of severe cases with COVID-19: a meta-analysis
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 12 August 2020, e175
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COVID-19 in India: transmission dynamics, epidemiological characteristics, testing, recovery and effect of weather
-
- Journal:
- Epidemiology & Infection / Volume 148 / 2020
- Published online by Cambridge University Press:
- 11 August 2020, e182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LARGE SAMPLE PROPERTIES OF BAYESIAN ESTIMATION OF SPATIAL ECONOMETRIC MODELS
-
- Journal:
- Econometric Theory / Volume 37 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 11 August 2020, pp. 708-746
-
- Article
- Export citation
EFFICIENT DYNAMIC HEDGING FOR LARGE VARIABLE ANNUITY PORTFOLIOS WITH MULTIPLE UNDERLYING ASSETS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 50 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 11 August 2020, pp. 913-957
- Print publication:
- September 2020
-
- Article
- Export citation
JOINT TIME-SERIES AND CROSS-SECTION LIMIT THEORY UNDER MIXINGALE ASSUMPTIONS
-
- Journal:
- Econometric Theory / Volume 38 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 11 August 2020, pp. 942-958
-
- Article
- Export citation