Let a, b, c be fixed coprime positive integers with 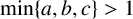 $\min \{a,b,c\}>1$. We discuss the conjecture that the equation
$\min \{a,b,c\}>1$. We discuss the conjecture that the equation 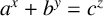 $a^{x}+b^{y}=c^{z}$ has at most one positive integer solution
$a^{x}+b^{y}=c^{z}$ has at most one positive integer solution 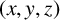 $(x,y,z)$ with
$(x,y,z)$ with 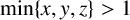 $\min \{x,y,z\}>1$, which is far from solved. For any odd positive integer r with
$\min \{x,y,z\}>1$, which is far from solved. For any odd positive integer r with 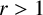 $r>1$, let
$r>1$, let 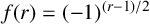 $f(r)=(-1)^{(r-1)/2}$ and
$f(r)=(-1)^{(r-1)/2}$ and 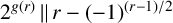 $2^{g(r)}\,\|\, r-(-1)^{(r-1)/2}$. We prove that if one of the following conditions is satisfied, then the conjecture is true: (i)
$2^{g(r)}\,\|\, r-(-1)^{(r-1)/2}$. We prove that if one of the following conditions is satisfied, then the conjecture is true: (i) 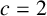 $c=2$; (ii) a, b and c are distinct primes; (iii)
$c=2$; (ii) a, b and c are distinct primes; (iii) 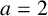 $a=2$ and either
$a=2$ and either 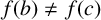 $f(b)\ne f(c)$, or
$f(b)\ne f(c)$, or 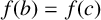 $f(b)=f(c)$ and
$f(b)=f(c)$ and 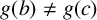 $g(b)\ne g(c)$.
$g(b)\ne g(c)$.
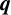 $\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
$\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
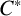 $\mathbf{\mathit{C}}^{*}$-ALGEBRAS WHICH DETECT NUCLEARITY
$\mathbf{\mathit{C}}^{*}$-ALGEBRAS WHICH DETECT NUCLEARITY
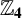 $\ \boldsymbol {\mathbb {Z}_{4}}$
$\ \boldsymbol {\mathbb {Z}_{4}}$