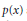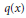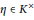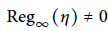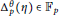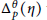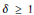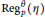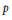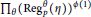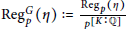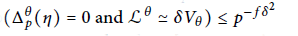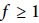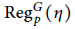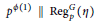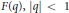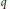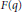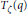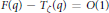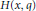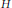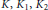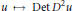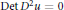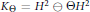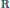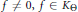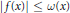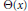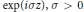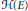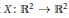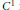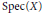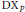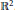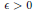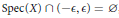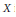Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 23
Strong Asymptotics of Hermite-PadéApproximants for Angelesco Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1159-1200
-
- Article
-
- You have access
- Export citation
- Cited by 23
Certain Varieties and Quasivarieties of Completely Regular Semigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1171-1197
-
- Article
-
- You have access
- Export citation
- Cited by 23
Polynomes a Valeurs Entieres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 747-754
-
- Article
-
- You have access
- Export citation
- Cited by 23
Representation of Linear Functionalson Köthe Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 568-575
-
- Article
-
- You have access
- Export citation
- Cited by 23
On Two-faced Families of Non-commutative Random Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1290-1325
-
- Article
-
- You have access
- Export citation
- Cited by 23
Transfer of Fourier Multipliers into Schur Multipliers and Sumsets in a Discrete Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1161-1187
-
- Article
-
- You have access
- Export citation
- Cited by 23
Mahler’s Measure and the Dilogarithm (I)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 468-492
-
- Article
-
- You have access
- Export citation
- Cited by 22
Les θ-régulateurs locaux d'un nombre algébrique : Conjectures p-adiques
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 571-624
-
- Article
-
- You have access
- Export citation
- Cited by 22
Embeddings of L-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 513-558
-
- Article
-
- You have access
- Export citation
- Cited by 22
The H and K Family of Mock Theta Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 935-960
-
- Article
-
- You have access
- Export citation
- Cited by 22
Some Rigidity Results Related to Monge–Ampère Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 320-354
-
- Article
-
- You have access
- Export citation
- Cited by 22
Admissible Majorants for Model Subspaces of H 2, Part II: Fast Winding of the Generating Inner Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1264-1301
-
- Article
-
- You have access
- Export citation
- Cited by 22
Level Raising and Anticyclotomic Selmer Groups for Hilbert Modular Forms of Weight Two
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 588-668
-
- Article
-
- You have access
- Export citation
- Cited by 22
Monotone Hurwitz Numbers in Genus Zero
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1020-1042
-
- Article
-
- You have access
- Export citation
- Cited by 22
Simple Proofs of Some Theorems on High Degrees of Unsolvability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1072-1080
-
- Article
-
- You have access
- Export citation
- Cited by 22
On the Injectivity of C 1 Maps of the Real Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1187-1201
-
- Article
-
- You have access
- Export citation
- Cited by 22
Minorations de Combinaisons Linéaires de Logarithmes de Nombres Algébriques
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 176-224
-
- Article
-
- You have access
- Export citation
- Cited by 22
Topological Properties of the Set of Norm-Attaining Linear Functionals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 318-329
-
- Article
-
- You have access
- Export citation
- Cited by 22
Spectral Asymptotics of Laplacians Associated with One-dimensional Iterated Function Systems with Overlaps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 648-688
-
- Article
-
- You have access
- Export citation
- Cited by 22
On the Fundamental Lemma for Standard Endoscopy: Reduction to Unit Elements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 974-994
-
- Article
-
- You have access
- Export citation