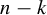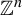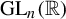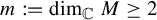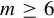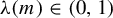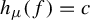Contents
Original Article
Equidistribution of rational subspaces and their shapes
- Part of:
-
- Published online by Cambridge University Press:
- 10 November 2023, pp. 2009-2062
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random and mean Lyapunov exponents for
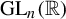 $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2063-2079
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mechanism for ejecting a horseshoe from a partially hyperbolic chain recurrence class
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2023, pp. 2080-2142
-
- Article
- Export citation
On the ergodicity of unitary frame flows on Kähler manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2023, pp. 2143-2172
-
- Article
- Export citation
Smooth models for certain fibered partially hyperbolic systems
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2023, pp. 2173-2198
-
- Article
- Export citation
Markov capacity for factor codes with an unambiguous symbol
- Part of:
-
- Published online by Cambridge University Press:
- 07 November 2023, pp. 2199-2228
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2229-2256
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conditional intermediate entropy and Birkhoff average properties of hyperbolic flows
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2023, pp. 2257-2288
-
- Article
- Export citation
Stabilized automorphism group of odometers and of Toeplitz subshifts
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2023, pp. 2289-2307
-
- Article
- Export citation
Constructing Birkhoff sections for pseudo-Anosov flows with controlled complexity
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2023, pp. 2308-2360
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 44 issue 8 Cover and Front matter
-
- Published online by Cambridge University Press:
- 23 September 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 44 issue 8 Cover and Back matter
-
- Published online by Cambridge University Press:
- 23 September 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation