Contents
Research Article
Ergodic optimization of super-continuous functions on shift spaces
-
- Published online by Cambridge University Press:
- 14 October 2011, pp. 2071-2082
-
- Article
- Export citation
Recurrence rates for observations of flows
-
- Published online by Cambridge University Press:
- 06 September 2011, pp. 1727-1751
-
- Article
- Export citation
ℤd-actions with prescribed topological and ergodic properties
-
- Published online by Cambridge University Press:
- 12 April 2011, pp. 191-209
-
- Article
- Export citation
Generalized Hausdorff dimensions of sets of real numbers with zero entropy expansion
-
- Published online by Cambridge University Press:
- 19 September 2011, pp. 1073-1089
-
- Article
- Export citation
Tail pressure and the tail entropy function
-
- Published online by Cambridge University Press:
- 14 June 2011, pp. 1400-1417
-
- Article
- Export citation
New spectral multiplicities for mixing transformations
-
- Published online by Cambridge University Press:
- 14 March 2011, pp. 517-534
-
- Article
- Export citation
On the entropy of actions of nilpotent Lie groups and their lattice subgroups
-
- Published online by Cambridge University Press:
- 21 October 2011, pp. 535-573
-
- Article
- Export citation
Summable formal invariant curves of diffeomorphisms
-
- Published online by Cambridge University Press:
- 14 March 2011, pp. 211-221
-
- Article
- Export citation
Dynamical approximation and kernels of non-escaping hyperbolic components
-
- Published online by Cambridge University Press:
- 14 June 2011, pp. 1418-1434
-
- Article
- Export citation
Convergence of moments for Axiom A and non-uniformly hyperbolic flows
-
- Published online by Cambridge University Press:
- 10 June 2011, pp. 1091-1100
-
- Article
- Export citation
Contact Anosov flows and the Fourier–Bros–Iagolnitzer transform
-
- Published online by Cambridge University Press:
- 03 November 2011, pp. 2083-2118
-
- Article
- Export citation
Rigidity of commutative non-hyperbolic actions by toral automorphisms
-
- Published online by Cambridge University Press:
- 16 September 2011, pp. 1752-1782
-
- Article
- Export citation
Non-uniqueness in
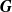 -measures
-measures
-
- Published online by Cambridge University Press:
- 16 September 2011, pp. 575-586
-
- Article
- Export citation
Discontinuity of topological entropy for Lozi maps
-
- Published online by Cambridge University Press:
- 16 September 2011, pp. 1783-1800
-
- Article
- Export citation
Stable topological transitivity properties of ℝn-extensions of hyperbolic transformations
-
- Published online by Cambridge University Press:
- 13 June 2011, pp. 1435-1443
-
- Article
- Export citation
Continuity of packing measure functions of self-similar iterated function systems
-
- Published online by Cambridge University Press:
- 24 May 2011, pp. 1101-1115
-
- Article
- Export citation
Transitivity of Heisenberg group extensions of hyperbolic systems
-
- Published online by Cambridge University Press:
- 05 April 2011, pp. 223-235
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 32 issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 November 2012, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
ETS volume 32 issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 November 2012, pp. b1-b8
-
- Article
-
- You have access
- Export citation
Research Article
A special case of effective equidistribution with explicit constants
-
- Published online by Cambridge University Press:
- 14 March 2011, pp. 237-247
-
- Article
- Export citation
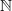 such that 1∈
such that 1∈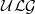 of connected, simply connected nilpotent Lie groups which contains ℝ
of connected, simply connected nilpotent Lie groups which contains ℝ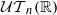 of all triangular unipotent matrices over ℝ and many of its subgroups, and is closed under direct products. If
of all triangular unipotent matrices over ℝ and many of its subgroups, and is closed under direct products. If 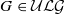 , then
, then 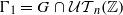 is a lattice subgroup of
is a lattice subgroup of 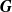 -measures
-measures