We study the acoustic behaviour of a mixture of diethyl-ether bubbles and liquid, at small volume fraction of vapour, contained in a standing-wave tube. We give experimental evidence of the effect of the liquid/vapour phase transition on the positions and amplitudes of the resonances of the tube. The effective-medium theory, which properly describes the behaviour of liquid/gas mixtures, is shown to be inadequate. We find that theoretical studies which take the effect of the phase transition into account do agree with our experimental data.

The linearized equations for wave motion of frequency ω in a shallow, viscous liquid of variable depth h are reduced to a partial differential equation. [Lscr]Z = 0, for the complex amplitude Z of the free-surface displacement on the assumptions of no slip at the bottom and Kh, Kδ* [Lt] 1, where K = ω2/g, and δ* = (ν/2ω)½ is a viscous lengthscale. It is shown that capillarity must be included in order to avoid an irregular singular point (which would imply the total absorption of an incoming wave) at h = 0. [Lscr]Z then is fourth-order and has a regular singular point of exponents 2, 1, 0, 0 for h ∼ σx ↓ 0. The requirements that the free-surface displacement and the shear force be bounded as h ↓ 0 rule out the solutions of exponent 0 and imply a stationary contact line. This last prediction is supported by laboratory observation but is not consistent with the observed runup of long, non-breaking waves on real beaches (for which the condition of no slip presumably must be relaxed). The dissipation for sufficiently small capillarity and viscosity is equal to that calculated from a boundary-layer approximation (despite the violation of the assumption h [Gt] δ* on which that approximation is based). The viscous modification of the Stokes edge wave on a uniform, gentle slope is calculated through matched asymptotic approximations to the solution of [Lscr]Z = 0.

An instability mechanism that can amplify wind-forced inertial oscillations in the upper ocean is investigated. This forced instability happens because of the phase relationship between the mixed-layer depth and the surface current. It allows the inertial oscillations propagating against the wind to extract energy from it and amplify. The key ingredients for the instability to work are (a) a non-zero mean wind stress, (b) a spatial variability of the oscillations in the direction of the wind stress. The amplification is demonstrated using a simple shallow-water model in a few situations: the dispersion of a localized disturbance with steady and time-varying wind forcing, generation of inertial waves at a coast, and spatial variability induced by mesoscale eddies. Estimates of the growth rate are provided for both dissipative and non-dissipative cases.

An incompressible inviscid flow theory for single and two-element airfoils experiencing trailing-edge stall is presented. For the single airfoil the model requires a simple sequence of conformal transformations to map a Joukowsky airfoil, partially truncated on the upper surface, onto a circle over which the flow problem is solved. Source and doublet singularities are used to create free streamlines simulating shear layers bounding the near wake. The model's simplicity permits extension of the method to airfoil-flap configurations in which trailing-edge stall is assumed on the flap. Williams’ analytical method to calculate the potential flow about two lifting bodies is incorporated in the Joukowsky-arc wake-singularity model to allow for flow separation. The theoretical pressure distributions from these models show good agreement with wind-tunnel measurements.

Unsteady spatially localized states such as puffs, slugs or spots play an important role in transition to turbulence. In plane Couette flow, steady versions of these states are found on two intertwined solution branches describing homoclinic snaking (Schneider et al., Phys. Rev. Lett., vol. 104, 2010, 104501). These branches can be used to generate a number of spatially localized initial conditions whose transition can be investigated. From the low Reynolds numbers where homoclinic snaking is first observed ($Re<175$) to transitional ones ($Re\approx 325$), these spatially localized states traverse various regimes where their relaminarization time and dynamics are affected by the dynamical structure of phase space. These regimes are reported and characterized in this paper for a $4\unicode[STIX]{x03C0}$-periodic domain in the streamwise direction as a function of the two remaining variables: the Reynolds number and the width of the localized pattern. Close to the snaking, localized states are attracted by spatially localized periodic orbits before relaminarizing. At larger values of the Reynolds number, the flow enters a chaotic transient of variable duration before relaminarizing. Very long chaotic transients ($t>10^{4}$) can be observed without difficulty for relatively low values of the Reynolds number ($Re\approx 250$).

We generalize the linear stability analysis of the axisymmetric self-similar solution of gravity currents from finite-volume releases to include perturbations that depend on both radial and azimuthal coordinates. We show that the similarity solution is stable to sufficiently small perturbations by proving that all perturbation eigenfunctions decay in time. Moreover, asymmetric perturbations are shown to decay more rapidly than axisymmetric perturbations in general. An asymptotic formula for the eigenvalues is derived, which indicates that asymptotic rates of decay of perturbations are given by $t^{-\sigma}$ where $0\,{<}\,\sigma\,{<}\,\frac{1}{4}$ as the Froude number decreases from $\sqrt2$ to $0$. We demonstrate that this formula agrees closely with numerically calculated eigenvalues and, in the absence of azimuthal dependence, it reduces to an expression that improves on the asymptotic formula obtained by Grundy & Rottman (1985). For two-dimensional (planar) currents, we further prove analytically that all perturbation eigenfunctions decay like $t^{-{1/2}}.$

Transversely homogeneous, uniformly sheared, turbulent flow was allowed to reach its asymptotic structure in a straight wind tunnel section and then it was passed through a sequence of two curved sections and a final straight section. The cross-sectional shape of the entire wind tunnel was rectangular, while the two curved sections had circular centrelines with the same radius but opposing curvatures. In all cases, the mean strain rate due to curvature was relatively weak (±5%), compared to the mean shear rate, but its effects on the turbulence kinetic energy and structure were substantial; streamwise pressure gradient effects were negligible. The turbulence structure approached approximately self-similar states towards the downstream ends of each curved section but the main interest of the present study was the rate of adjustment of the turbulence following a stepwise change in curvature. It has been shown that the adjustment of the shear stress anisotropy, which is a sensitive indicator of structural changes, can be approximated by a first-order system response, whose time constant scales with the inverse mean shear and is independent of the curvature parameter. Uniformly sheared flow results were used for an interpretation of the structure of curved turbulent boundary layers, both during adjustment and in a fully developed state.

We present a method for calculating the hydrodynamic interactions between particles in the kinetic (or transition regime), characterized by non-negligible particle Knudsen numbers. Such particles are often present in aerosol systems. The method is based on our extended Kirkwood–Riseman theory (Corson et al., Phys. Rev. E, vol. 95 (1), 2017c, 013103), which accounts for interactions between spheres using the velocity field around a translating sphere as a function of Knudsen number. Results for the two-sphere problem at small Knudsen numbers are in good agreement with those obtained using Felderhof’s interaction actions for mixed slip-stick boundary conditions, which are accurate to order $r^{-7}$ (Felderhof, Physica A, vol. 89 (2), 1977, pp. 373–384). The strength of the interactions decreases with increasing Knudsen number. Results for two fractal aggregates demonstrate that one can apply a point force approach for interactions between particles in the transition regime; the interaction tensor is similar to the Oseen tensor for continuum flow. Using this point force approach, we present an analysis for the settling of an unbounded cloud of particles. Our analysis shows that for sufficiently high volume fractions and cloud radii, the cloud behaves as a gas droplet in continuum flow even when the individual particles are small relative to the mean free path of the gas. The method presented here can be applied in a Brownian dynamics simulation analogous to Stokesian dynamics to study the behaviour of a dense aerosol system.

The interaction of a point vortex with a layer of constant vorticity, bounded below by a wall and above by an irrotational flow, is investigated as a model of vortex–boundary layer interaction. This model calculates both the evolution of the interface which separates the vortex layer from the irrotational flow and the trajectory of the vortex. In order to determine the conditions which lead to sustained unsteady interaction, three cases are investigated where the mutual interaction between the vortex and interface is initially assumed to be weak. (i) When a weak point vortex lies outside the layer, the vortex moves with a horizontal speed that is small relative to the long-wave phase speed of interfacial waves. A uniformly valid solution is found for the interface evolution. This solution shows that for long times the interface and the vortex approach an equilibrium state. (ii) When a weak vortex lies inside the layer, the vortex is convected by the mean flow and moves with a horizontal speed which matches the phase speed of an interfacial wave. This results in a strong interaction between the vortex and the interfacial wave. On the interface, a monochromatic wavetrain forms upstream of the vortex and acts to attract or repel the point vortex. The displacement of the vortex due to the wavetrain results in the modulation of the amplitude and wavelength of the wavetrain. If the point vortex is attracted toward the interface the horizontal speed of the vortex slows and disturbances directly above the vortex focus and grow leading to the ejection of vorticity. (iii) When the point vortex lies close to the wall and it is sufficiently strong it propagates downstream with a large horizontal velocity. In this case, the amplitude of the interfacial disturbance is independent of the vortex strength. Again, the vortex and the interface approach an equilibrium state. The results of this paper indicate that when the horizontal speed of the vortex matches the phase speed of the interfacial disturbance, it is necessary to account for the vertical displacement of the vortex in order to predict the behaviour of vortex–boundary layer interactions.

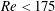
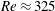
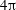
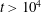
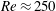
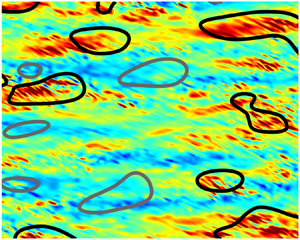
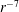
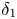
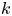
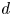
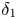
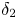
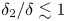
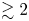
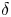
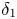
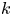
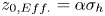
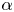
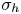
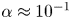
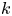
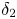
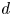
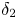
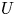
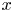
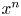
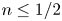
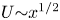
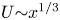
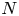
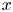
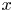
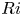
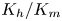
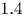
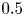
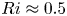
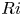
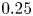
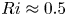
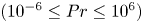
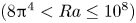
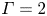
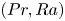
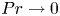
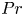
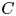
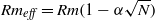The influence of an externally applied magnetic field on flow turbulence is investigated in liquid-gallium von-Kármán (VK) swirling flows. Time-resolved measurements of global variables (such as the flow power consumption) and local recordings of the induced magnetic field are made. From these measurements, an effective Reynolds number is introduced as , so as to take into account the influence of the interaction parameter 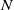. This effective magnetic Reynolds number leads to unified scalings for both global variables and the locally induced magnetic field. In addition, when the flow rotation axis is perpendicular to the direction of the applied magnetic field, significant flow and induced magnetic field fluctuations are observed at low interaction parameter values, but corresponding to an Alfvèn speed 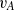of the order of the fluid velocity fluctuations 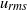. This strong increase in the flow fluctuations is attributed to chaotic changes between hydrodynamic and magnetohydrodynamic velocity profiles.

We investigate the statistical properties of Lagrangian tracers transported by a time-correlated compressible renewing flow. We show that the preferential sampling of the phase space performed by tracers yields significant differences between the Lagrangian statistics and its Eulerian counterpart. In particular, the effective compressibility experienced by tracers has a non-trivial dependence on the time correlation of the flow. We examine the consequence of this phenomenon on the clustering of tracers, focusing on the transition from the weak- to the strong-clustering regime. We find that the critical compressibility at which the transition occurs is minimum when the time correlation of the flow is of the order of the typical eddy turnover time. Further, we demonstrate that the clustering properties in time-correlated compressible flows are non-universal and are strongly influenced by the spatio-temporal structure of the velocity field.

We consider the linear stability to axisymmetric perturbations of the family of inviscid vortex rings discovered by Norbury (J. Fluid Mech., vol. 57, 1973, pp. 417–431). Since these vortex rings are obtained as solutions to a free-boundary problem, their stability analysis is performed using recently developed methods of shape differentiation applied to the contour-dynamics formulation of the problem in the three-dimensional axisymmetric geometry. This approach allows us to systematically account for the effects of boundary deformations on the linearized evolution of the vortex ring. We investigate the instantaneous amplification of perturbations assumed to have the same the circulation as the vortex rings in their equilibrium configuration. These stability properties are then determined by the spectrum of a singular integro-differential operator defined on the vortex boundary in the meridional plane. The resulting generalized eigenvalue problem is solved numerically with a spectrally accurate discretization. Our results reveal that while thin vortex rings remain neutrally stable to axisymmetric perturbations, they become linearly unstable to such perturbations when they are sufficiently ‘fat’. Analysis of the structure of the eigenmodes demonstrates that they approach the corresponding eigenmodes of Rankine’s vortex and Hill’s vortex in the thin-vortex and fat-vortex limit, respectively. This study is a stepping stone on the way towards a complete stability analysis of inviscid vortex rings with respect to general perturbations.

Recent linear stability analyses of double-diffusive convection in a laterally heated vertical slot containing water have shown that for very weak (or no) vertical salinity gradient the initial instabilities are steady, but as the salinity gradient is increased there is a transition to oscillatory instabilities. For higher Prandtl number fluids the initial instabilities in a slot with no stratification can be oscillatory or wave-like. We show that the oscillatory instabilities in water are linked to these higher Prandtl number oscillatory instabilities. The salinity gradient has a destabilizing effect on these oscillations, making them appear for Prandtl numbers where oscillatory instabilities are not possible in the absence of salinity gradients. We derive an asymptotic description for this mode of instability.

A land- and sea-breeze (LSB) circulation under a calm stably stratified environment was simulated in the laboratory using a temperature-controlled water tank. The floor of the tank was divided into two sections representing land and sea. Two heat exchangers, each of them connected to a thermostat, simulated the diurnal thermal cycle typically experienced by the surface in coastal zones. A third heat exchanger positioned at the top of the tank provided a stable thermal stratification. Particle-tracking velocimetry was applied to evaluate the two-dimensional velocity field in the vertical centreline section of the tank orthogonal to the coastline, while a rack of thermocouples measured the vertical temperature profile near the coastline and further inland. It is shown that the overall flow consists of a closed circulation caused by the periodic change of the horizontal temperature difference between land and sea surfaces. Furthermore, the formations of cellular convection during the first phase of warming of the land-side as well as the genesis of the sea-breeze front were detected and analysed. Application of the proper orthogonal decomposition (POD) technique allowed the vortical large-scale structures in the flow to be determined. The results suggest that the energy contained in the first POD eigenmodes rapidly converged with the first mode, associated with the overall LSB circulation, being dominant with 73% of the energy. The other less energetic modes were mainly associated with the cellular convection.

The interaction of weak shock waves with small heterogeneities in gaseous media is studied. It is first shown that various linear theories proposed for this problem lead to pathological breakdowns or singularities in the solution near the wavefront and necessarily fail to describe this interaction. Then, a nonlinear small-disturbance model is developed. The nonlinear theory is uniformly valid and accounts for the competition between the near-sonic speed of the wavefront and the small variations of vorticity and sound speed in the heterogeneous media. This model is an extension of the transonic small-disturbance problem, with additional terms accounting for slight variations in the media. The model is used to analyse the propagation of the sonic-boom shock wave through the turbulent atmospheric boundary layer. It is found that, in this instance, the nonlinear model accounts for the observed behaviour. Various deterministic examples of interaction phenomena demonstrate good agreement with available experimental data and explain the main observed phenomena in Crow (1969).