We investigate a novel geometric Iwasawa theory for 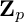 ${\mathbf Z}_p$-extensions of function fields over a perfect field k of characteristic
${\mathbf Z}_p$-extensions of function fields over a perfect field k of characteristic 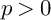 $p>0$ by replacing the usual study of p-torsion in class groups with the study of p-torsion class group schemes. That is, if
$p>0$ by replacing the usual study of p-torsion in class groups with the study of p-torsion class group schemes. That is, if 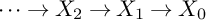 $\cdots \to X_2 \to X_1 \to X_0$ is the tower of curves over k associated with a
$\cdots \to X_2 \to X_1 \to X_0$ is the tower of curves over k associated with a 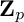 ${\mathbf Z}_p$-extension of function fields totally ramified over a finite nonempty set of places, we investigate the growth of the p-torsion group scheme in the Jacobian of
${\mathbf Z}_p$-extension of function fields totally ramified over a finite nonempty set of places, we investigate the growth of the p-torsion group scheme in the Jacobian of 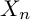 $X_n$ as
$X_n$ as 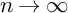 $n\rightarrow \infty $. By Dieudonné theory, this amounts to studying the first de Rham cohomology groups of
$n\rightarrow \infty $. By Dieudonné theory, this amounts to studying the first de Rham cohomology groups of 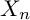 $X_n$ equipped with natural actions of Frobenius and of the Cartier operator V. We formulate and test a number of conjectures which predict striking regularity in the
$X_n$ equipped with natural actions of Frobenius and of the Cartier operator V. We formulate and test a number of conjectures which predict striking regularity in the 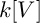 $k[V]$-module structure of the space
$k[V]$-module structure of the space 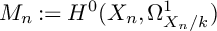 $M_n:=H^0(X_n, \Omega ^1_{X_n/k})$ of global regular differential forms as
$M_n:=H^0(X_n, \Omega ^1_{X_n/k})$ of global regular differential forms as 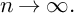 $n\rightarrow \infty .$ For example, for each tower in a basic class of
$n\rightarrow \infty .$ For example, for each tower in a basic class of 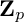 ${\mathbf Z}_p$-towers, we conjecture that the dimension of the kernel of
${\mathbf Z}_p$-towers, we conjecture that the dimension of the kernel of 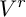 $V^r$ on
$V^r$ on 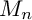 $M_n$ is given by
$M_n$ is given by 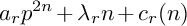 $a_r p^{2n} + \lambda _r n + c_r(n)$ for all n sufficiently large, where
$a_r p^{2n} + \lambda _r n + c_r(n)$ for all n sufficiently large, where 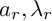 $a_r, \lambda _r$ are rational constants and
$a_r, \lambda _r$ are rational constants and 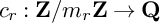 $c_r : {\mathbf Z}/m_r {\mathbf Z} \to {\mathbf Q}$ is a periodic function, depending on r and the tower. To provide evidence for these conjectures, we collect extensive experimental data based on new and more efficient algorithms for working with differentials on
$c_r : {\mathbf Z}/m_r {\mathbf Z} \to {\mathbf Q}$ is a periodic function, depending on r and the tower. To provide evidence for these conjectures, we collect extensive experimental data based on new and more efficient algorithms for working with differentials on 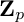 ${\mathbf Z}_p$-towers of curves, and we prove our conjectures in the case
${\mathbf Z}_p$-towers of curves, and we prove our conjectures in the case 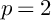 $p=2$ and
$p=2$ and 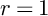 $r=1$.
$r=1$.
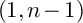 $(1,n-1)$
$(1,n-1)$