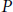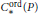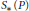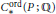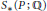Contents
Research Article
Semi-Classical Wavefront Set and Fourier Integral Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-263
-
- Article
-
- You have access
- Export citation
Correction
Erratum to: An Exactly Solved Model for Recombination, Mutation and Selection
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 264-265
-
- Article
-
- You have access
- Export citation
Research Article
Invariants and Coinvariants of the Symmetric Group in Noncommuting Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-296
-
- Article
-
- You have access
- Export citation
Transitive Factorizations in the Hyperoctahedral Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-312
-
- Article
-
- You have access
- Export citation
Asymptotic Properties for Increments of
 ${{l}^{\infty }}$ -Valued Gaussian Random Fields
${{l}^{\infty }}$ -Valued Gaussian Random Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-333
-
- Article
-
- You have access
- Export citation
Low-Pass Filters and Scaling Functions for Multivariable Wavelets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 334-347
-
- Article
-
- You have access
- Export citation
Monoidal Functors, Acyclic Models and Chain Operads
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 348-378
-
- Article
-
- You have access
- Export citation
Finite Cohen–Macaulay Type and Smooth Non-Commutative Schemes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 379-390
-
- Article
-
- You have access
- Export citation
The Geometry of the Weak Lefschetz Property and Level Sets of Points
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 391-411
-
- Article
-
- You have access
- Export citation
Quelques calculs de traces compactes et leurs transformées de Satake
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 412-442
-
- Article
-
- You have access
- Export citation
On a Class of Projectively Flat Metrics with Constant Flag Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 443-456
-
- Article
-
- You have access
- Export citation
Harmonic Coordinates on Fractals with Finitely Ramified Cell Structure
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 457-480
-
- Article
-
- You have access
- Export citation