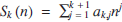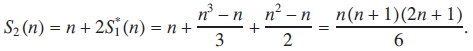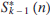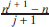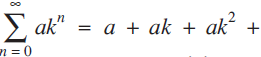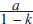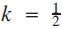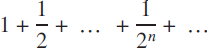Refine listing
Actions for selected content:
1418337 results in Open Access
Complex Earth–outer space systems and new spacetime for international law
-
- Journal:
- International Journal of Law in Context / Volume 21 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 300-313
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Australian shuffle and two self-working card tricks
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 303-307
- Print publication:
- July 2025
-
- Article
- Export citation
109.28 A trick with the gamma function
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 342-344
- Print publication:
- July 2025
-
- Article
- Export citation
Development of Evidence-based Guidelines on Assessment and Management of Internal Contamination with Transuranic Actinides
-
- Journal:
- Disaster Medicine and Public Health Preparedness / Volume 19 / 2025
- Published online by Cambridge University Press:
- 20 June 2025, e156
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poor mental health does not always reduce political participation: Wrong assumption, wrong samples, or wrong measures?
-
- Journal:
- Politics and the Life Sciences / Volume 44 / Issue 2 / Fall 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 247-259
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Standardless quantification of crystalline polymorphic mixtures using the component decomposition method
-
- Journal:
- Powder Diffraction , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-5
-
- Article
- Export citation
The most concise recurrence formula for the sums of integer powers
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 253-258
- Print publication:
- July 2025
-
- Article
- Export citation
Five mathematical gobbets
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 286-293
- Print publication:
- July 2025
-
- Article
- Export citation
Melissa Reynolds, Reading Practice: The Pursuit of Natural Knowledge from Manuscript to Print Chicago: University of Chicago Press, 2024. Pp. 318. ISBN 978-0-226-83489-4. $35.00 (paperback).
-
- Journal:
- The British Journal for the History of Science , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
109.27 A weighted Hölder’s inequality
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 341-342
- Print publication:
- July 2025
-
- Article
- Export citation
Sums of sums of geometric and related series
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 209-216
- Print publication:
- July 2025
-
- Article
- Export citation
Access to Legal Aid for Accused Persons with Disabilities in Kenya’s Criminal Justice System: An Outcomes-based Approach
-
- Journal:
- Journal of African Law , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variations of the Vecten configurations
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 265-272
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- Export citation
109.18 Transitivity, transpositions and permutation groups
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 317-318
- Print publication:
- July 2025
-
- Article
- Export citation
109.17 Covering a Hex Number with Octagonal Numbers
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 316-317
- Print publication:
- July 2025
-
- Article
- Export citation
Probably overthinking it by Allen B. Downey , pp 252, £20 (paper), ISBN 978-022682-258-7, University of Chicago Press (2023)
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 375-377
- Print publication:
- July 2025
-
- Article
- Export citation
109.22 A constant function
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 331-332
- Print publication:
- July 2025
-
- Article
- Export citation
109.26 A simple self-improvement of the Cauchy-Schwarz inequality
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 338-341
- Print publication:
- July 2025
-
- Article
- Export citation
For a history of human rationality: an interview with Lorraine Daston. 2024 Balzan Prize for History of Modern and Contemporary Science
-
- Journal:
- The British Journal for the History of Science , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Feedback
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, p. 353
- Print publication:
- July 2025
-
- Article
-
- You have access
- Export citation
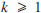 , let
, let