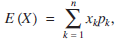Refine listing
Actions for selected content:
1418337 results in Open Access
Transcatheter reduction of a large, stented fenestration in a paediatric patient post-Fontan palliation
-
- Journal:
- Cardiology in the Young / Volume 35 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1082-1084
-
- Article
- Export citation
Real Analysis by Gustavo Da Silva Araüjo , Luis Bernal Gonzalez , Jose L. Gamez Merino , Maria E. Martinez Gomez , Gustavo A. Munoz Fernandez , Daniel L. Rodriguez Vidanesand Sepülveda Juan B. Seoane et al, pp 536, £43.99 (paper), ISBN 978-1-03251-026-2, Routledge/Taylor & Francis/CKC Press (2024)
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 374-375
- Print publication:
- July 2025
-
- Article
- Export citation
Is math real? by Eugenia Cheng , pp 336, £9.99 (paper), ISBN 978-1-54160-182-6, Basic Books (2023).
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 367-369
- Print publication:
- July 2025
-
- Article
- Export citation
MATHEMATICAL MODELLING AND ANALYSIS OF HARMFUL ALGAL BLOOM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 389-391
- Print publication:
- October 2025
-
- Article
-
- You have access
- HTML
- Export citation
Actions of groups, a second course in algebra by John McCleary , pp. 226, £29.99 (paper), ISBN 978-1-00915-811-4, Cambridge University Press (2023)
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 371-372
- Print publication:
- July 2025
-
- Article
- Export citation
Smoothing surfaces on fourfolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Power of Patristic Preaching: The Word in Our Flesh by Andrew HoferOP, Foreword by Paul M. Blowers, The Catholic University of America Press, Washington, DC, 2023, pp. xxiii + 389, pbk $34.95
-
- Journal:
- New Blackfriars / Volume 106 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 457-458
- Print publication:
- September 2025
-
- Article
- Export citation
Hunt for solutions to a problem of Euler
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 199-208
- Print publication:
- July 2025
-
- Article
- Export citation
109.16 PWW (Proof Without Words): The largest side of a triangle corresponds to the smallest median
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, p. 316
- Print publication:
- July 2025
-
- Article
- Export citation
Big-5 personality traits and their dynamic and conditional effects on COVID-19 attitudes and behaviors
-
- Journal:
- Politics and the Life Sciences / Volume 44 / Issue 2 / Fall 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 205-231
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Jules Skotnes-Brown, Segregated Species: Pests, Knowledge, and Boundaries in South Africa, 1910–1948 Baltimore: Johns Hopkins University Press, 2024. Pp. 344. ISBN 978-1-4214-4856-5. $64.95 (hardcover).
-
- Journal:
- The British Journal for the History of Science , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Mathematical Puzzles (2nd edition) by Peter Winkler, pp 450, £20.79, ISBN 978-1-03270-848-5, Routledge/Taylor & Francis/CKC Press (2024)
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, p. 383
- Print publication:
- July 2025
-
- Article
- Export citation
A caution (or two) regarding mathematical expectation
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 247-252
- Print publication:
- July 2025
-
- Article
- Export citation
109.23 The derivative of the integral, redux
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 332-334
- Print publication:
- July 2025
-
- Article
- Export citation
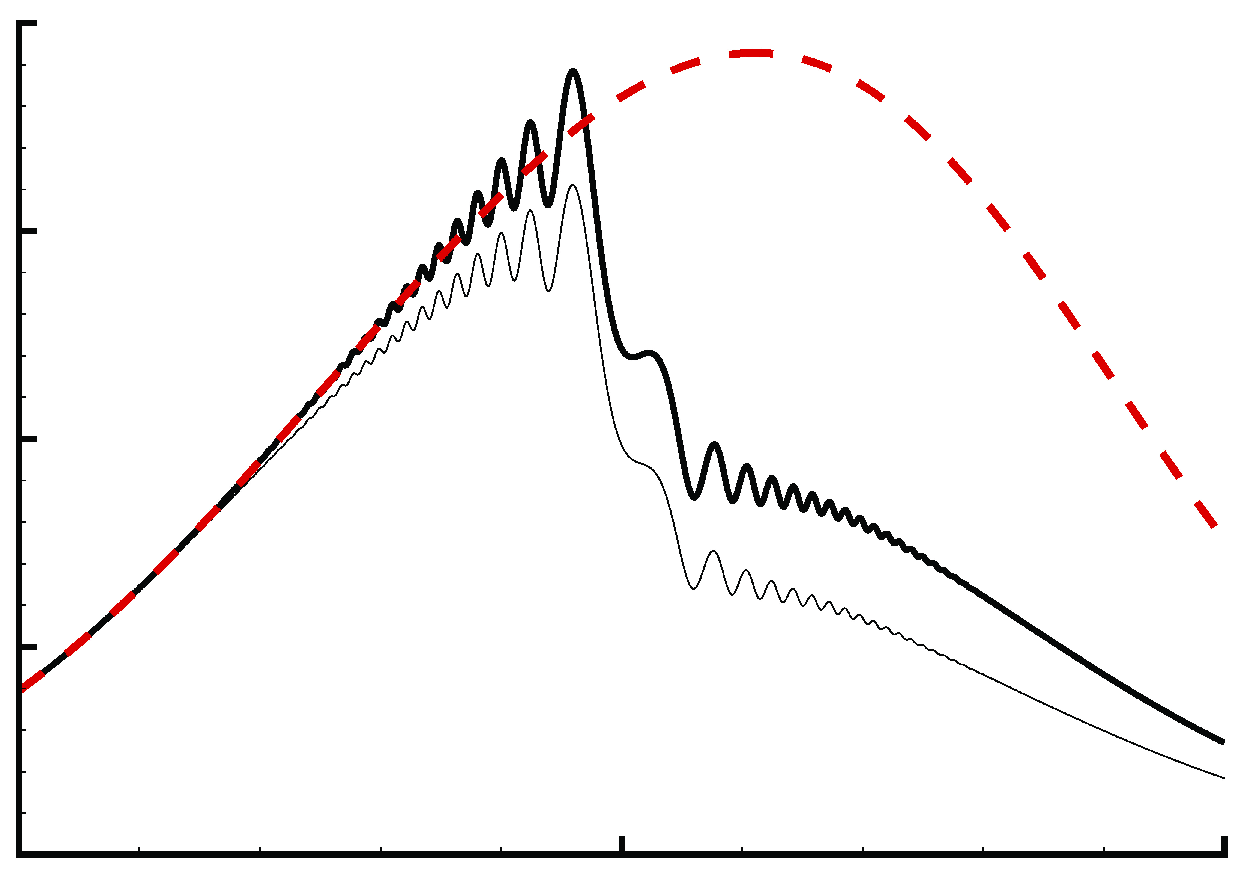
Nonlinear evolution of radiating modes in the presence of sound waves impinging on a supersonic boundary layer: subharmonic resonance
-
- Journal:
- Journal of Fluid Mechanics / Volume 1013 / 25 June 2025
- Published online by Cambridge University Press:
- 20 June 2025, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Language in the age of AI technology: From human to non-human authenticity, from public governance to privatised assemblages
-
- Journal:
- Language in Society , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Laws of the Land: Fengshui and the State in Qing Dynasty China By Tristan G. Brown. Princeton: Princeton University Press, 2023. 356pp. $45 (cloth), $29.95 (paper), $45 (eBook)
-
- Journal:
- Journal of Chinese History , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-3
-
- Article
- Export citation
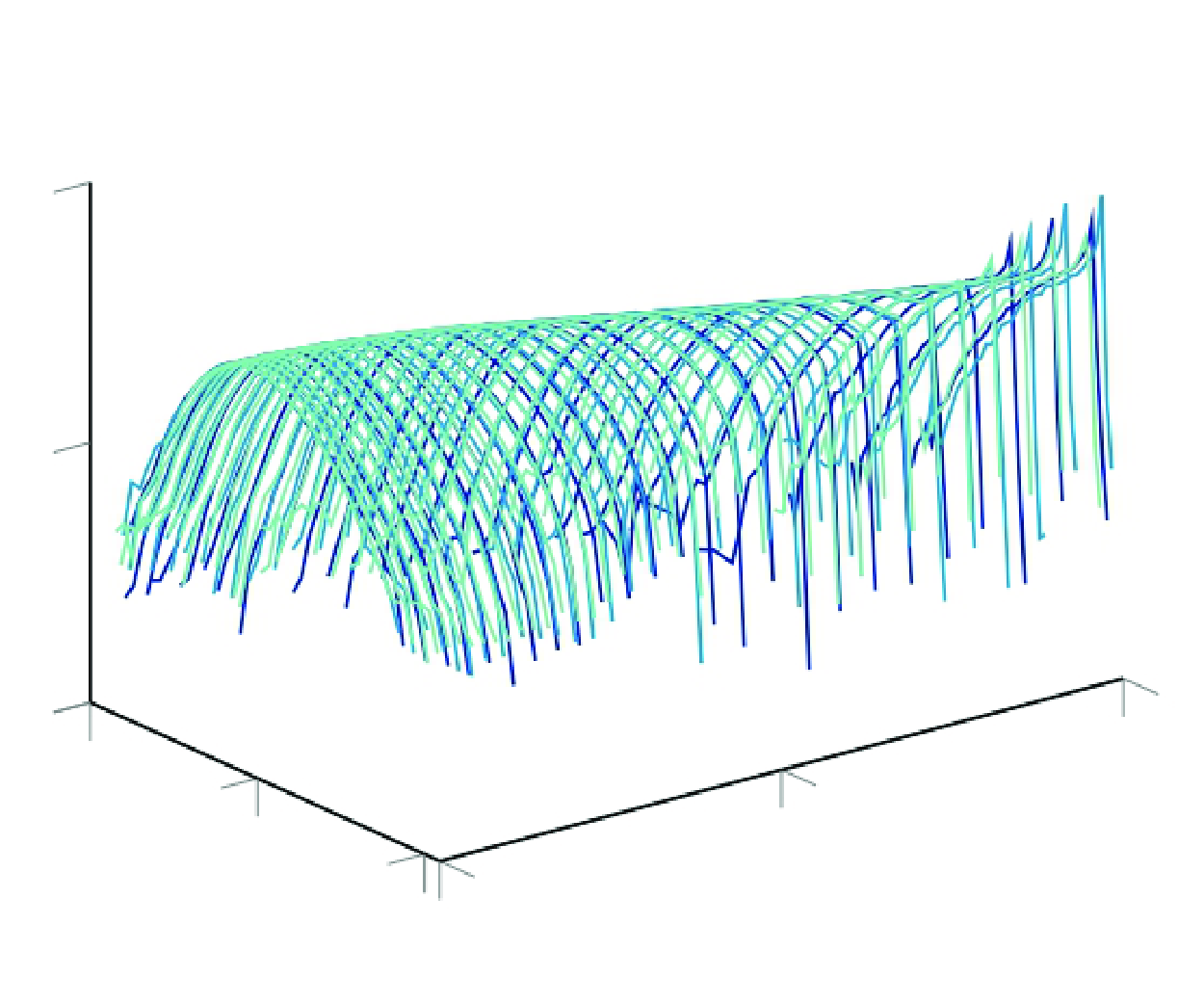
Passive scalar statistics in a turbulent round jet: symmetry theory and direct numerical simulation
-
- Journal:
- Journal of Fluid Mechanics / Volume 1013 / 25 June 2025
- Published online by Cambridge University Press:
- 20 June 2025, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
109.31 Did Tindley know the Archimedean property of
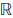 $$\mathbb R$$?
$$\mathbb R$$?
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, p. 352
- Print publication:
- July 2025
-
- Article
- Export citation
Approximation of the value of π using metallic means and the unit hyperbola
-
- Journal:
- The Mathematical Gazette / Volume 109 / Issue 575 / July 2025
- Published online by Cambridge University Press:
- 20 June 2025, pp. 193-198
- Print publication:
- July 2025
-
- Article
- Export citation